2017-12-14
4180
Рассмотрим электрон, находящийся в так называемой " потенциальной яме ". Под эти понимается, что на отрезке 0 < х < а (внутри ямы или, как ещё иногда говорят, ящика) потенциальная энергия энергия электрона неизменна и конечна, например, равна нулю (U(x) = 0),а вне этого отрезка при х < 0 и х> а и на его границах при х = 0 и х = а потенциальная энергия обращается в бесконечность.
При описанных условиях одномерное стационарное уравнение Шредингера (16) можно записать в виде
Поскольку потенциальная энергия по условию равна нулю, то полная энергия Е в этом уравнении равна кинетической энергии частицы (электрона).
Конечно символика частной производной здесь лишняя, но не будем ничего менять, просто помним, что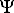 
зависит только от одной переменной — х.
Преобразуем множитель перед 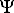-функцией:
 | (27) |
Тогда получаем
 | (28) |
Здесь 
— не что иное, как длина волны де Бройля для электрона.
Решения уравнения (28) будут иметь вид
| 1) |   | (29) |
| 2) |   | (30) |
По условию частица не может находиться вне ящика, поэтому её волновая функция на границах ящика при х = 0 и х = а равна нулю, то есть 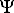(0) = 0 и 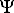(а) = 0.
Согласно этим граничным условиям при х = 0 из (30) следует, что 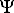= В. Это означает, что длина волны 
может быть любой, так как при х = а должно быть 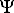= 0. Поэтому
 | , | (31) |
здесь, n = 1, 2, 3,...
Следовательно
 | (32) |
| С учётом (32) из (29) имеем |  | (33) |
Используя условие нормировки (26) для 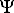-функции вида (33) можно записать (в условия потенциального ящика интегрирование ведётся от 0 до а)
| Определив отсюда значение постоянной |  | , получаем |
| вид волновой функции для частицы в бесконечно глубоком прямоугольном потенциальном ящике |
 | (34) |
Теперь, зная вид волновой функции уже можно проанализировать поведение частицы внутри ящика.
На рис.6 (а) на основании формулы (34) приведены графики функции 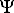n(x), а на рис.6 (б) графики плотности вероятности | 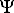n(x)|2 обнаружения частицы внутри ящика для трёх значений квантового числа n.
| а) | б) |
| Рис. 6 |
Из рис.6(б) следует, что, например, при значении квантового числа n = 2, частица равновероятно может находиться вблизи стенок ящика, а вот вероятность её обнаружения в его центре равна нулю.
Такое поведение частицы говорит о том, что понятие координаты, а значит и траектории движения частицы, в квантовой механике не существует.
