Способы решения навигационных задач

Выберем способ местоопределения. Наиболее широкое распространение получили графический, аналитический и итерационный способы. Наглядным является графический способ решения навигационной задачи на поверхности [14-16].

7.5.1 Графический метод решения навигационной задачи по измеряемым дальностям на плоскости.

Каким-либо способом определяются дальности навигационных приёмников от трёх навигационных точек d ₁, d ₂ и d ₃ , имеющих известные координаты x_j, y_j в Декартовой системе координат.

1) Строится графическое представление Декартовой системы координат.

2) Задается масштаб по осям абсцисс и ординат 50 км = 1см.

3) На график наносится местоположение навигационных точек.

4) Из заданных положений навигационных точек проводятся отрезки пересекающихся окружностей с радиусами d ₁, d ₂ и d ₃.

5) Точка пересечения построенных пересекающихся отрезков окружностей будет соответствовать местоположению приёмника (метод засечек).

6) Координаты приёмника определяются по проекциям точки пересечения построенных линий на осях Декартовой системы координат.

7.5.2 Графический способ решения навигационных задач в трёхмерном пространстве.

Допустим, что потребитель определил своё удаление d ₁ от единственной НТ₁. Для определения своего местоположения потребитель использует Декартовую систему координат для плоскости с ортогональными осями X и Y, направленными на восток В и север С соответственно. Тогда потребитель может изобразить на плоскости окружность с радиусом d ₁ , центр которой размещен в координатах геометрической точки НТ₁. По единственной сфере потребитель может сказать себе, что он находится в какой-то неизвестной точке на сфере.

По измерениям удаления от трёх навигационных точек потребитель определяет свои координаты в пространстве.

Значит, для определения координат и высоты расположения потребителя навигационная системы должна иметь как минимум три навигационные точки. Правда в этом случае ещё не решается задача учета временного сдвига синхрогенераторов приемника и передатчиков. Эту задачу можно решить включением в навигационную систему четвертой навигационной точки НТ₄. Тогда также методом итерации с добавлением или вычитанием времени расхождения синхрогенераторов задача местоопределения решается полностью.

Итак, для решения любых задач навигации система должна обладать четырьмя навигационными точками. Тогда решается пространственная задача с определением и высоты расположения приёмника над уровнем моря.

Описанный выше метод называется параболическим методом определения местоположения.

7.5.3 Аналитический способ решения задач навигации.

Исходные параметры для расчётов удаления приёмника R от навигационной точки Т можно представить следующим образом.

В полярной системе координат удаление приёмника от передатчика d определяется из разности векторов OТ-OR находим:

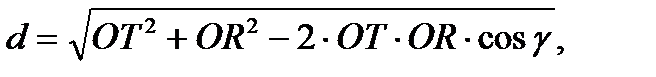
где g - угол между приёмником и передатчиком,

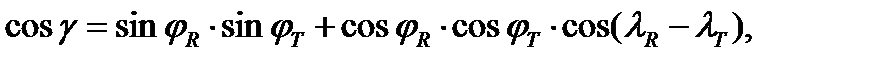
ОТ = R _Å+ h_{Т ,} OR = R _Å + h_R.

Зная координаты ИСЗ в геоцентрической системе, можно вычи­слить значения азимута А и угла места g для любой точки раз­мещения ЗС. Если считать Землю идеальным шаром, возвышение станции над уровнем моря нулевым, а спутник расположенным в плоскости экватора с периодом, точно равным звездным суткам (гео­стационарный ИСЗ), то азимут и угол места для луча антенны ЗС можно вычислить по формулам:

;

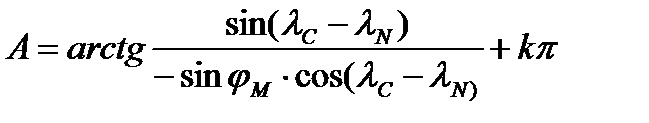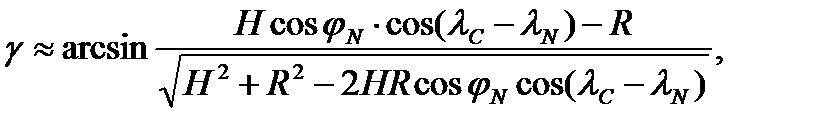
где l _c— долгота подспутниковой точки спутника в относительной геоцентрической системе координат;

H» 42 170 км — высота орбиты над центром Земли;

R= 6371 км — радиус Земли;

k = 0 при g_N< 0, l _c> l_N;

k = 2 при j_N< 0, l _c< l_N;

k = 1 при j_N> 0.

По определенному значению угла места можно найти границу зоны видимости ИСЗ. Эта граница определяется условием g> 0.

В декартовой системе координат эта за­дача выражается в виде системы четырёх уравнений, описывающих окружности с центрами, расположенными в навигационных точках. Произведём преобразование полярных координат в составляющие декартовой системы. Здесь мы имеем:

OA = OB = R _Å - средний радиус Земли = 6371 м;

h_R = AR и h_S = BТ – высоты приёмника и навигационной точки над поверхностью Земли;

X, Y, Z – оси ортогональных геоцентрических (декартовых) координат;

Z_Т = (h_Т + R _Å)×sin j_Т;

L _Т = (h_Т + R _Å)×cos j_Т;

Z_R = (h_R + R _Å)×sin j_R;

L_R = (h_R + R _Å)×cos j_R;

X_Т = L_Т ×cos l_Т;

Y_Т = L_Т ×sin l_Т;

X_R = L_R ×cos l_R;

Y_R = L_S ×sin l_R,

где j и l - широта и долгота;

Z и L – проекции векторов на вертикальную ось и экваториальную плоскость геоцентрической декартовой системы координат.

Для определения теперь уже трёх искомых значений осевых проекций Х_R, Y_R, Z_R точки R понадобится решать сис­тему из четырёх уравнений:

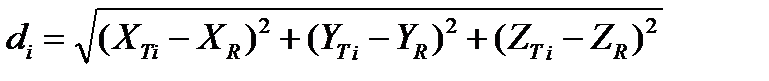, i =1, 2, 3, 4.

7.5.4 Разностно-дальномерные РНС.

Разностно-дальномерные РНС, относящиеся к радиотехничес­ким системам дальней навигации, определяют навига­ционный параметр р= d_A-d_B, где d_A и d_B - расстояния объекта от двух РНТ.

В качестве параметра можно взять разность расстоя­ний от подвижной точки до двух неподвижных. Полу­чаем разностно-дальномерное устройство. В простей­шем случае радиопередатчики опорных точек должны излучать синхронно радиоимпульсы, а на подвижной точке следует иметь приёмник и измерять интервал вре­мени между моментами приёма двух сигналов. Уравне­ние параметра d_Б -d_A =c ( t - t_k) = 2 a.

Поверхностью положения будет гиперболоид, образо­ванный вращением гиперболы вокруг оси ОХ.

(x/a)² - (y/b) ²- (z/b)² = 1

b= [(d/ 2)² – a² ]^1/2,

где а и b - полуоси.

Поскольку d /2< a, то полуоси действительные. При разных значениях параметра получим семейство гипер­бол.

При увеличении рас­стояния гипербола стремится к асимптоте y = ± bx/a.

Положение асимптоты можно характеризовать углом (q), отсчитывая его от перпендикуляра к базе. Тогда уравнение запишем так: y = ± bx/a = x ctg q.

Описанный выше метод называется гиперболическим методом определения местоположения.

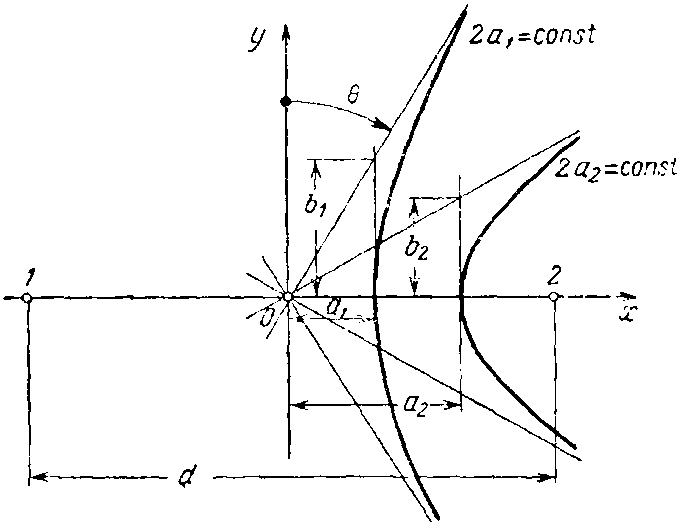
Рисунок 7.1 - Линии положения на плоскости разностно-дальномерного устройства