2017-12-14
866
Теорема. Если при переходе через точку х 0производная дифференцируемой функции у =f (х) меняет свой знак с плюса на минус, то точка х 0есть точка максимума функции у =f (х), а если с минуса на плюс,–то точка минимума.
Схема исследования функции у =f (х) на экстремум.
1. Найти производную 
.
2. Найти критические точки функции, в которых производная 
или не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4. Найти экстремумы (экстремальные значения) функции.
Пример 2. Исследовать на экстремум функцию 
Решение.
1. Производная функции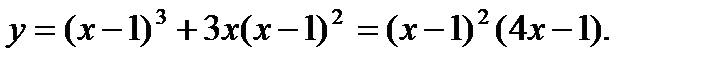 
2. Приравнивая производную к нулю, находим критическиеточки функции 
; х 2 = 1. (Точек, в которых производнаяне существует, у данной функции нет – 
определена на всей числовой оси).
3. Нанесем критические точки на кривую прямую (см. рис.).
Для определения знака производной слева и справа от критической точки 
выберем, например, значения 
и 
и найдем 
и 
следовательно, 
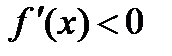при всех 
и 
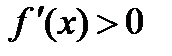на интервале 
.
|
|
|
Аналогично устанавливаем, что 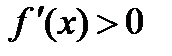и на интервале 
.
Согласно достаточному условию – точка минимума данной функции. В точке 
экстремума нет.
4. Находим 
