Второе достаточное условие экстремума

Теорема. Если первая производная дважды дифференцируемой функции равна нулю в некоторой точке х ₀, а вторая производная в этой точке положительна, то х ₀есть точка минимума функции ; если отрицательна, то х ₀– точка максимума.

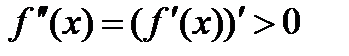Пусть , а . Это значит, что f"(x) = (f' (x)) ' > 0 также и в некоторой окрестности точки х ₀, т.е. 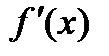возрастает на некотором интервале (а,b), содержащем точку х ₀.

Но , следовательно, на интервале (а,х ₀) , а на интервале (х ₀, b) , т.е. при переходе через точку х ₀ меняет знак с минуса на плюс, т.е. х ₀– точка минимума.

Аналогично рассматривается случай и .

Схема исследования на экстремум функции у =f (х) с помощью второго достаточного условия в целом аналогична схеме, приведенной выше (совпадают полностью пп. 1, 2, 4). Отличие в п. 3, устанавливающем наличие экстремума: здесь необходимо найти вторую производную и определить ее знак в каждой критической точке.