2017-12-14
1034
Согласно теореме Вейерштрасса, если функция у =f (х) непрерывна на отрезке [ а, b ], то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значение функцииможет достигаться как и точках экстремума, так и в точках на концах отрезка.
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную 
.
2. Найти критические точки функции, в которых 
или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее 
и наименьшее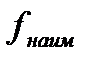 
.
Пример 1. Найти наибольшее и наименьшее значения функции 
на отрезке [0; 5].
Решение.
1. 
2. , откуда критические точки 
и х 2 = 4.
3. Значение функции в критических точках f (2)=0, 
и на концах отрезка f (0)=4 и 
. Итак, 
, 
Замечание. Если функция у =f (х) непрерывна на интервале (а, b), то она может не принимать на нем наибольшее и наименьшее значения. В частном случае, если дифференцируемая функция на интересе (а, b) имеет лишь одну точку максимума (ши одну точку минимума), то наибольшее (ши наименьшее) значение функции совпадает с максимумом (ши минимумом) этой функции.
|
|
|
Например, на интервале (1; 2) функция у=х 2– 6 х + 5 имеет один минимум 
, следовательно, это и есть наименьшее значение функции 
. Заметим, что наибольшего значения данная функция на указанном интервале не имеет.
