Экстремум функции и интервалы монотонности

Функция у = f (х) называется возрастающей (убывающей) на промежутке X, если для любых верно неравенство

Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка X, то она возрастает на этом промежутке.

Рассмотрим два значения х₁ и х₂ на данном промежутке X. Пусть . Докажем,

Для функции f(x) на отрезке [ х₁; х₂ ] выполняются условия теоремы Лагранжа, поэтому

,

где , т.е. 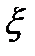принадлежит промежутку, на котором производная положительна, откуда следует, что и правая часть равенства положительна. Отсюда и

 

Аналогично доказывается другая теорема.

 

Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка X, то она убывает на этом промежутке.

 

Геометрическая интерпретация условия монотонности функции приведена на рисунке 7.

Если касательные к кривой в некотором промежутке направлены под острыми углами к оси абсцисс (рис. 7а), то функция возрастает, если под тупыми (рис. 7 б), то убывает.

 

Рисунок 7 – Геометрическая интерпретация условия монотонности функции

Пример 1. Найти интервалы монотонности функции у = х ²– 4 х + 3.

Решение. Имеем Очевидно при х > 2и у' < 0 при х < 2, т.е. функция убывает на интервале и возрастает на интервале где х ₀ = 2 — абсцисса вершиныпараболы.

 

Заметим, что необходимое условие монотонности более слабое. Если функция возрастает (убывает) на некотором промежутке X, то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке: т.е. в отдельных точках производная монотонной функции может равняться нулю.

 

Пример 2. Найти интервалы монотонности функции у = х ³.

 

Решение. Найдем производную Очевидно, что у > 0 при . При х = 0 производная обращается в нуль. Функция же монотонно возрастает на всей числовой оси.

Экстремум функции

 

Определение 1. Точка х ₀называется точкой максимума функции f (х), если в некоторой окрестности точки х ₀выполняется неравенство

Определение 2. Точка х ₁, называется точкой минимума функции f (х), если в некоторой окрестности точки х ₁,выполняется неравенство

Значения функции в точках х ₀и х ₁, называются соответственно максимумом и минимумом функции.

Максимум и минимум функции объединяются общим названием экстремума функции.

Экстремум функции часто называют локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с достаточно малой окрестностью точки х_n. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой, например, на рисунке 8

Наличие максимума (или минимума) в отдельной точке промежутка X вовсе не означает, что в этой точке функция f (х) принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)).

Необходимое условие экстремума: Для того чтобы функция у =f (х) имела экстремум в точке х ₀, необходимо, чтобы ее производная в этой точке равнялась нулю () или не существовала.

Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются критическими (или стационарными).

Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.

Рисунок 8 – Экстремумы функции f (х)

 

Пример 1. Найти критические точки функции и убедиться в наличии или отсутствии экстремума в этих точках:

а) б) в)

Решение:

а) Производная В точке х =0 и действительно в точке х =0 функция имеет экстремум.

б) Функция также возрастает на всей числовой оси по свойству степенной функции. Производная в точке х =0, , но экстремума в точке х =0 нет (см. рис. 9).

в) Функция 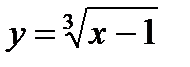также возрастает на всей числовой оси, производная при х =1 не существует, т.е. , но экстремума в этой точке нет (см. рис. 9).

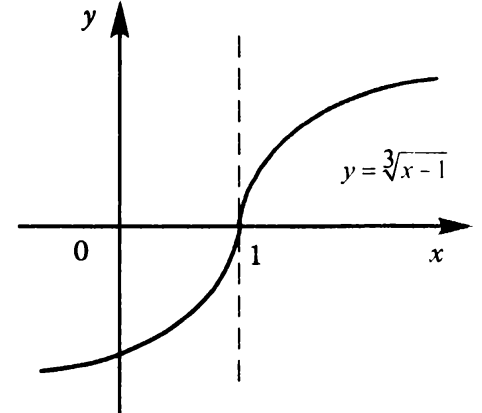
Рисунок 9 – Графики функций

 

Таким образом, для нахождения экстремумов функции требуется дополнительное исследование критических точек. Иными словами, требуется знать достаточное условие экстремума.