Уравнение касательной к кривой у = f (х) в точке x 0 примет вид
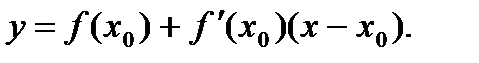
Алгоритм составления уравнения касательной к графику функции
1. Обозначить абсциссу точки касания буквой x 0.
2. Вычислить f (х 0).
3. Найти 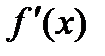 и вычислить
и вычислить 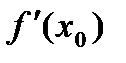 .
.
4. Подставить найденные числа x 0, f (х 0),  в формулу
в формулу 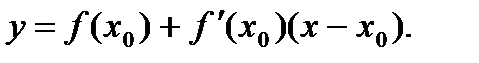
Пример 1. Составить уравнение касательной к графику функции  в точке x =1.
в точке x =1.
Решение:
Воспользуемся алгоритмом, учитывая, что 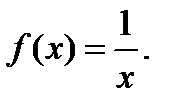
1. x 0=1.
2. 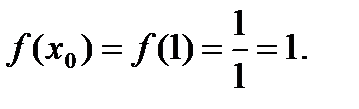
3. 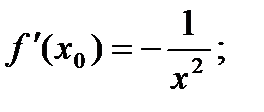

4. Подставим найденные числа в формулу.
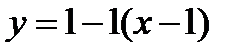 ;
;
y =2– x.
Ответ: y =2– x.
На рисунке 6 изображена гипербола  , построенная прямая y =2– x.
, построенная прямая y =2– x.
Рисунок 6 – гипербола 

Пример 2. К графику функции 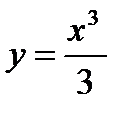 провести касательную так, чтобы она была параллельна прямой y =4 x –5.
провести касательную так, чтобы она была параллельна прямой y =4 x –5.
Решение. Чтобы провести касательную к функции необходимо найти составить ее уравнение. Искомая касательная должна быть параллельна прямой y =4 x –5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: k = 4, а 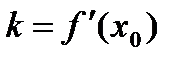 .
.
Таким образом, значение x 0мы можем найти из уравнения 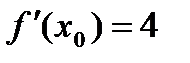 .
.
Имеем: 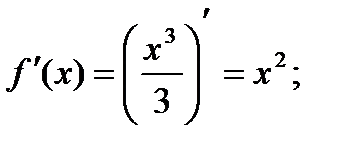
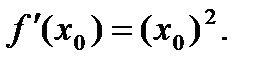
Из уравнения 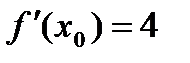 , т.е.
, т.е.  , находим: x1=2, x2=-2. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
, находим: x1=2, x2=-2. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.
Далее действуем по алгоритму.
1. x 1=2, x 2=-2.
2. 
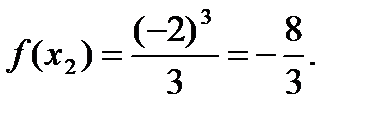
3. 
4. Подставим значения x 1=2, 
 в формулу и получим
в формулу и получим 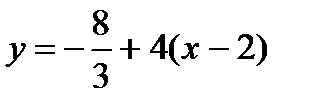 , т.е.
, т.е. 
Подставим значения x 2 = –2, 
 в формулу и получим
в формулу и получим 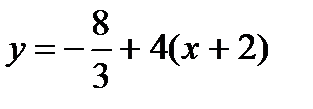 , т.е.
, т.е. 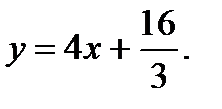
Ответ: 
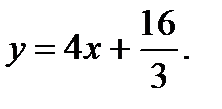
 2017-12-14
2017-12-14 1981
1981
