2017-12-14
8686
При исследовании функций и построении их графиков рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функцию на четность – нечетность.
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения графика с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Пример 1. Исследовать функцию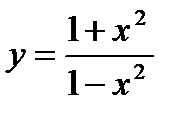 
и построить ее график.
Решение.
1. Область определения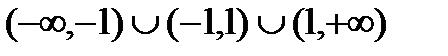 
, т.е. 
.
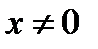2. Функция четная, так как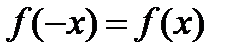 
, и ее график симметричен относительно оси ординат.
3. Вертикальные асимптоты могут пересекать ось абсцисс в точках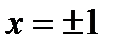 
. Так как пределы функции при 
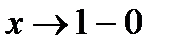(слева) и при 
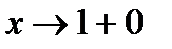(справа) бесконечны, т.е.
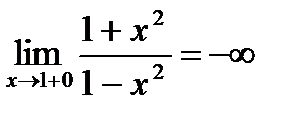и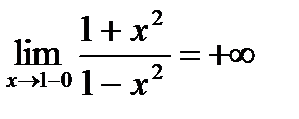 
, то прямая х = 1 естьвертикальная асимптота. В силу симметрии графика f (х) х = –1 также вертикальная асимптота.
4. Поведение функции в бесконечности. Вычислим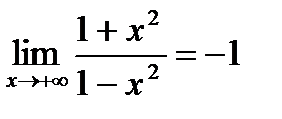 
.
В силу четности имеем также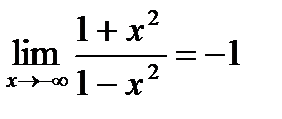 
, т.е. прямая у = – 1 – горизонтальная асимптота.
5. Экстремумы и интервалы монотонности.
Найдем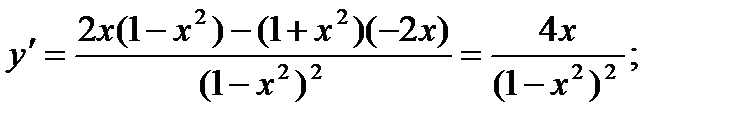 
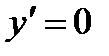при х = 0 и 
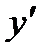не существует при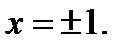 
Однако критической является только точка х 1 = 0 (так как
значения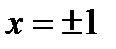 
не входят в область определения функции). Поскольку при х <0 
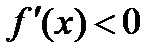, а при х > 0 
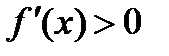(рис. 11), то x = 0 – точка минимума и 
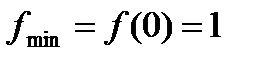– минимум функции.
На интервалах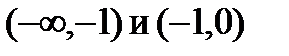 
функция убывает, на интервалах 
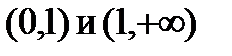– возрастает.
6. Интервалы выпуклости и точки перегиба.
Найдем
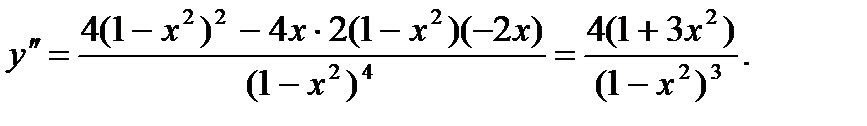
Очевидно, что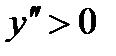 
на интервале (–1, 1) и функция выпукла вниз на этом интервале. 
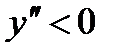на интервале 
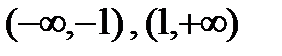, и на этих интервалах функция выпукла вверх. Точек перегиба нет.
7. Точки пересечения с осями.
f (0) = 1, т.е. точка пересечения с осью ординат (0, 1).
Уравнение f (х) = 0 решений не имеет, следовательно, график функции не пересекает ось абсцисс.
График функции изображен на рисунок 12.
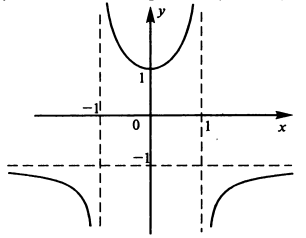
Рисунок 12 – График функции
Задания для самоконтроля
1. Вычислить производную функции:
а) 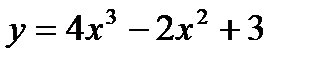 | и)  |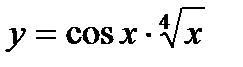
б) 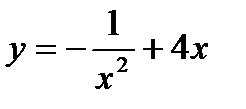 | к)  |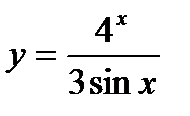
в) 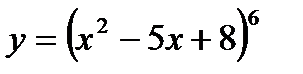 | л)  |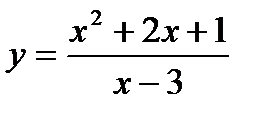
г) 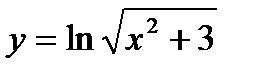 | м)  |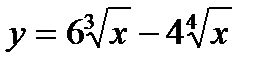
д) 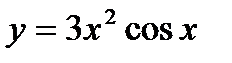 | н) у = (х 2+3)10 |
е) 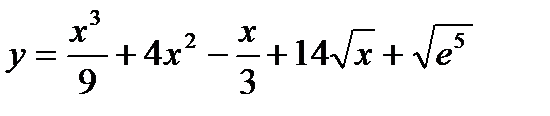 | о) y = sin8 x |
ж) 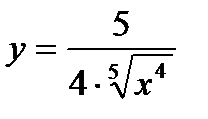 | п)  |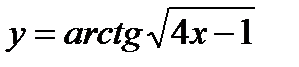
з) 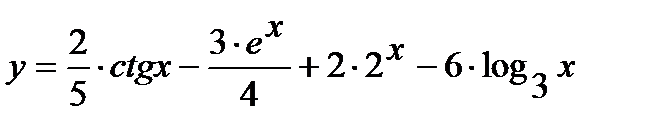 | р) у = ln sin x |
2.
а) Дана функция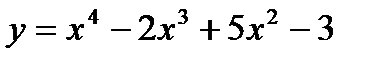 
. Найти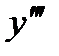 
б) Дана функция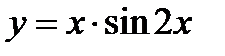 
. Найти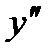 
3. Составить уравнение касательной к графику функции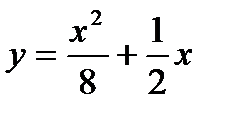 
, проходящей через точку х 0=2.
4. Исследовать функцию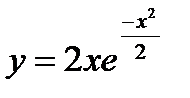 
и построить ее график.
