Пример 1.1 Пусть имеется выборка из 10 наблюдений (то есть N=10):
x1=5, x2=2, x3=4, x4=5, x5=7, x6=3, x7=6, x8=8, x9=3, x10=9.
Исследовать свойства одномерной случайной величины
Решение
1 Построение вариационного ряда (ряда распределения)
z1=2, z2=3, z3=3, z4=4, z5=5, z6=5, z7=6, z8=7, z9=8, z10=9.
2 Построение диаграммы накопленных частот
– на оси абсцисс отмечаем значения наблюдений 2, 3, 4, 5, 6, 7, 8, 9;
– затем откладываем значения по оси ординат.
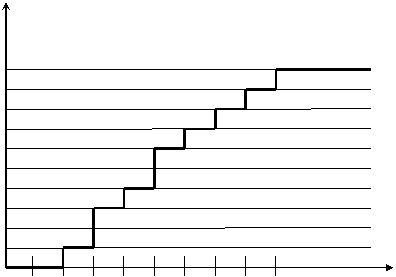
Левееxmin =2 значение ординаты равно нулю, а в точке x=2 диаграмма имеет скачок, равный 1/N=1/10. В данном примере в выборке присутствуют два значения x=3 и два значения x=5 ( λ=2), следовательно, в точках x=3 и x=5 на диаграмме происходит скачок, равный λ/N=2/10. В остальных точках выборки диаграмма имеет скачок, равный 1/N=1/10. Для величин x>xmax=9 значение диаграммы накопленных частот равно 1

1
9/10
8/10
7/10
6/10
5/10
4/10
3/10
2/10
1/10
x
1 2 3 4 5 6 7 8 9
Рисунок 1.1 – Построение диаграммы накопленных частот
3 Построение гистограммы выборки
K = 1 + 3,2lg10 = 1+3,2 = 4,2 ≈ 5,
∆x = (9 – 2) / 5 = 7/5 = 1,4,
(xmax+xmin)/2 = (9+2)/2 = 5,5 – центр распределения выборки, для данного примера при выбранном числе интервалов – это середина третьего интервала. Следовательно, слева и справа от этого значения необходимо отложить по 2,5 интервала или 2,5∆ x.
5,5
 x
x
 2 3,4 4,8 6,2 7,6 9
2 3,4 4,8 6,2 7,6 9
∆x
Рисунок 1.2 – Разбиение оси Ox на интервалы (кванты)
В первый интервал попало три значения zl N1=3, во второй – одно значение zl N2=1, в третий – три значения zl N3=3, в четвертый – одно значение zl N4=1, в пятый – два значения zl N5=2.
N=10, N1/N=3/10=0,3; N2/N=1/10=0,1; N3/N=3/10=0,3; N4/N=1/10=0,1; N5/N=2/10=0,2.
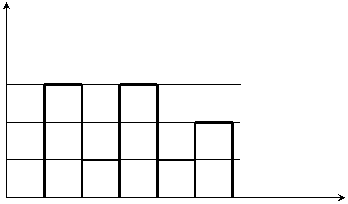
По результатам предыдущих этапов строим гистограмму для данного примера.
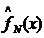
0,3
0,2
0,1
2 3,4 4,8 6,2 7,6 9 x
Рисунок 1.3 – Построение гистограммы выборки
4. Определение оценок математического ожидания,
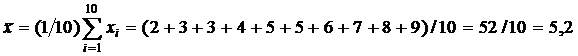
дисперсии
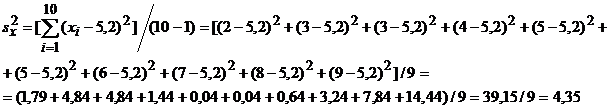
среднего квадратического отклонения:

Пример 1.2 Две установки должны напылять резисторы с одинаковыми сопротивлениями. При замере получены следующие данные (в Омах):
Установка 1 (Х1): 1095, 1025, 938, 915, 1012, 980, 975, 990, 1000, 974;
Установка 2 (Х2): 942, 938, 1010, 1030, 973, 915, 990, 970,925, 1045, 1100, 1020, 985, 1082, 1065, 1090.
Определить, одинаково ли налажены установки.
Решение. По формулам (1.22) и (1.23) определяем:
 1=987,7 Ом; s12=2587,12 Ом2 при
1=987,7 Ом; s12=2587,12 Ом2 при 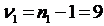 ,
,
 2=1005,0 Ом; s22=3605,73 Ом2 при
2=1005,0 Ом; s22=3605,73 Ом2 при 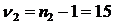 .
.
Затем по формулам (2.4) и (2.5) находим
S2=(9·2587,12+15·3605,73)/(9+15)=3223,75
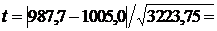 0,3049
0,3049
По таблице A1 приложения А находим tкр =2,06 ( =0,05;
=0,05; 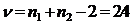 )
)
Так как tкр>t, то гипотеза о равенстве выборочных средних принимается, следовательно обе установки налажены одинаково.
Пример 1.3 Установка для напыления должна быть настроена на величину сопротивления напыляемых резисторов M(х)=15кОм. При замере получились следующие значения: 13,2; 14,7; 12,9; 15,3; 13,8; 14,1; 12,8; 16,8; 13,5; 14,2; 16,2; 14,1; 13,9; 14,3; 15,1кОм.
Определить правильность настройки.
Решение Определим среднее значение и стандартное отклонение полученной выборки по формулам (1.22) и (1.23)
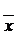 =13,5 кОм, s2=1,8973 кОм2 при
=13,5 кОм, s2=1,8973 кОм2 при 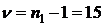
Так как величину 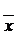 надо сравнить с постоянным числом, то размах Стьюдента подсчитывается по формуле
надо сравнить с постоянным числом, то размах Стьюдента подсчитывается по формуле
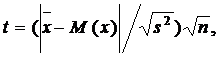 (1.29)
(1.29)
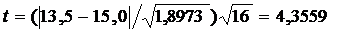
По таблице А1 приложения А при β=0,05, ν=15 находим tкр=2,13.
Так как tкр<t, то гипотеза о равенстве выборочного среднего значения сопротивления напыляемых резисторов заданным 15 кОм отвергается, следовательно установка для напыления настроена неправильно.
Пример 1.4 Определить границы существования истинного значения математического ожидания по условию примера 1.2 при доверительной вероятности P=0,95.
Решение Д ля коэффициента риска β=1–p=0,05 и степени свободы ν=15 величина критерия Стьюдента по таблице А1 приложения А tкр=2,13. Из формулы (1.29) и используя условие принятия критерия о равенстве двух средних: tкр>t, можно составить следующее неравенство
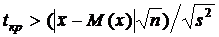 ,
,
Следовательно
 Подставляя числовые значения, получаем
Подставляя числовые значения, получаем
12,766 кОм < M(x) < 14,234 кОм
Пример 1.5 При измерении толщины слоя окисла после диффузии в большой партии пластин получилась следующая выборка: 30, 29, 28, 31, 34, 30, 28, 29, 29, 28, 30, 28, 31, 30, 29, 30, 28, 31, 30, 28, 28 мкм.
Определить наличие грубых ошибок.
Решение Грубой ошибкой измерения может быть только крайнее значение выборки, то есть в данном случае это 28 или 34 мкм. Так как значение 34 мкм встречается всего один раз, то сначала необходимо проверить его.
Задача сводится к сравнению двух средних выборок, одна из которых состоит из единственного подозреваемого значения, а вторая – из всех остальных. То есть надо сравнить выборку без подозреваемого значения с постоянным числом (этим подозреваемым значением).
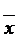 =29,25; s2=1,2204 при n=20.
=29,25; s2=1,2204 при n=20.
По формуле (2.5) для M(x)=34 получаем
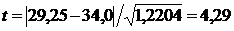
По таблице А1 приложения А при β=0,05, ν=n–1=19 находим tкр=2,14.
Так как tкр<t, то гипотеза о равенстве сравниваемых значений отвергается, следовательно подозреваемое значение является грубой ошибкой и должно быть исключено из дальнейшей статистической обработки.
Пример 1.6 Определить, одинакова или различна точность измерений двух выборок в примере 1.2.
Решение Согласно формуле (1.27) вычисляем критерий Фишера. Поскольку в числитель всегда ставится большее число, тогда в данном случае
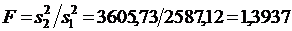
По таблице А2 приложения А при β = 0,05, νчисл = 15, νзнам = 9 находим Fкр=2,71. Так как Fкр>F, то гипотеза о равноточности измерений в обеих сериях опытов принимается.
Пример 1.7 В результате измерений четырех партий резисторов получены следующие данные
Таблица 1.1 – Исходные данные для примера 1.7
| Номер партии | Результаты измерений, кОм | ||||||||
| 1 | 12,1 | 11,7 | 11,9 | 11,9 | 12,1 | 11,8 | 12,3 | 12,0 | 11,6 |
| 2 | 14,5 | 14,7 | 14,9 | 15,2 | 14,6 | 15,3 | 15,6 | 15,1 | 14,9 |
| 3 | 19,3 | 20,1 | 20,7 | 19,5 | 19,8 | 20,3 | 20,4 | 19,4 | 20,5 |
| 4 | 26,1 | 27,3 | 27,8 | 26,5 | 26,8 | 27,3 | 27,1 | 27,6 | 26,7 |
Определить одинакова или различна точность измерений всех партий резисторов.
Решение Для каждой партии резисторов найдем средние арифметические значения и эмпирические дисперсии по формулам (1.22) и (1.23).

По формуле (2.7) вычисляем критерий Кохрена

По таблице А3 приложения А при β=0,05, νчисл=8, νзнам=4 находим Gкр=0,54. Так как Gкр>G, то можно считать, что все измерения во всех опытах сделаны равноточно, причем дисперсия измерений в среднем равна

Задачи для решения
В таблице 1.2 приведены значения выборочных измерений 10 партий напыляемых резисторов.
1. По заданной выборке, в которую входят результаты замеров i-той и j-той партий резисторов, исследовать свойства одномерной случайной величины.
2. Оцените расхождение средних значений сопротивлений между двумя партиями резисторов (номера партий приведены в таблице 1.3).
3. Определите правильность настройки на величину 1000 Ом установки для напыления резисторов, при условии что i-тая и j-тая партии напылялись на одной установке (табл. 1.3).
4. Определите границы существования истинного значения математического ожидания для выборки, в которую входят результаты замеров i-той и j-той партий резисторов при доверительной вероятности Р=0,95 (табл. 1.3).
5. Определите наличие грубых ошибок в общей выборке, состоящей из замеров двух партий резисторов (табл. 1.3).
6. Определите, одинакова или различна точность замеров i-той и j-той партий резисторов (табл. 1.3).
7. Определите, одинакова или различна точность замеров четырех партий резисторов (номера партий приведены в таблице 1.3).
Таблица 1.2 – Исходные данные для задач
| Номер партии | Результаты измерений, Ом | |||||||||
Таблица 1.3 – Номера партий для задач 1 – 7
| Номер варианта | Номера партий из таблицы 1.2 | |||||
| Задачи № 1– 6 | Задача № 7 | |||||
Контрольные вопросы
1. Дать определение случайной величины.
2. Дать определение одномерного интегрального и дифференциального законов распределения случайной величины и назвать их свойства.
3. Дать определение двумерного интегрального и дифференциального законов распределения случайных величин и назвать их свойства.
4. Какие числовые параметры наиболее часто используются в качестве мер расположения и рассеяния одномерной и двумерной совокупности случайных величин?
5. Каким образом производится построение вариационного ряда, диаграммы накопленных частот, гистограммы выборки одномерной случайной величины?
6. Каким образом производится построение поля рассеяния и составление таблицы распределения двумерной совокупности случайных величин?
7. Что такое статистическая гипотеза и на основании чего ее можно принять или отвергнуть?
8. В каких случаях применяется критерий Кохрена и как с его помощью можно оценить однородность дисперсий?
9. В каких случаях однородность дисперсий проверяется по критерию Кохрена, а в каких по критерию Бартлета?
10. Как с помощью критерия Фишера можно выяснить, относятся ли дисперсии случайных величин к одной генеральной совокупности или к разным?
11. Как проверяется гипотеза о равенстве двух выборочных средних значений случайной величины?
12. Что означает понятие «число степеней свободы»?
13. С помощью какого критерия оценивают соответствие экспериментального распределения случайной величины предполагаемому теоретическому закону распределения?
14. Как проверяется принадлежность случайной величины к рассматриваемой генеральной совокупности случайных величин?
 2017-12-14
2017-12-14 4100
4100
