Пусть имеется набор (выборка) экспериментальных данных x1, x2,…xN. Обработку этих данных для получения эмпирических характеристик одномерной СВ производят обычно в следующей последовательности.
1 Построение вариационного ряда (ряда распределения) Вариационный ряд z1, z2,…zN получают из исходных данных путем расположения xm (m=1,2,…,N) в порядке возрастания от xmin до xmax так, чтобы xmin= z1 ≤ z2 ≤…≤ zN = xmax.
2 Построение диаграммы накопленных частот. Диаграмма накопленных частот  является эмпирическим аналогом интегрального закона распределения. Диаграмму строят в соответствии с формулой
является эмпирическим аналогом интегрального закона распределения. Диаграмму строят в соответствии с формулой
 (1.16)
(1.16)
где μN (x) – число элементов в выборке, для которых значение xi < x.
При построении диаграммы на оси абсцисс указывают значения наблюдений xm (или zl). Значение по оси ординат равно нулю левее точки xmin и далее во всех других точках xm диаграмма имеет скачок равный 1/N. Если существует несколько совпадающих значений xm, то в этом месте на диаграмме происходит скачок, равный λ/N, где λ – число совпадающих точек. Для величин x > xmax значение диаграммы накопленных частот равно 1. При N → ∞  → F(x).
→ F(x).
3 Построение гистограммы выборки Гистограмма 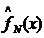 является эмпирическим аналогом функции плотности распределения f(x). Этапы построения гистограммы:
является эмпирическим аналогом функции плотности распределения f(x). Этапы построения гистограммы:
— Нахождение предварительного количества квантов (интервалов), на которое должна быть разбита ось Ox. Это количество К определяется с помощью оценочной формулы
K = 1 + 3,2lgN (1.17)
Найденное значение необходимо округлить до ближайшего целого.
— Определение длины интервала
∆x = (xmax – xmin) / K (1.18)
Величину ∆x можно округлить для удобства вычислений.
— Середину области изменения выборки (центр распределения) (xmax+xmin)/2 принимают за центр некоторого интервала, после чего определяют границы и окончательное количество указанных интервалов так, чтобы в совокупности они перекрывали всю область от xmin до xmax.
— Подсчет количества наблюдений Nm, попавших в каждый квант: Nm равно числу членов вариационного ряда, для которых справедливо неравенство
xm ≤ zl < xm + ∆x,
где xm и xm + ∆x – границы m-го интервала. Значения zl, попавшие на границу между (m-1)–м и m –м интервалами, относят к m –му интервалу.
— Подсчет относительного количества (относительной частоты) наблюдений Nm/N, попавших в данный квант.
— Построение гистограммы, которая представляет собой ступенчатую кривую, значение которой на m –м интервале (xm, xm + ∆x) постоянно и равно Nm/N.
4 Определение оценок математического ожидания  , дисперсии
, дисперсии  и среднего квадратического отклонения
и среднего квадратического отклонения 
 (1.19)
(1.19)
 (1.20)
(1.20)
 . (1.21)
. (1.21)
 2017-12-14
2017-12-14 1396
1396








