Матричное задание циклических кодов

Циклический код может быть задан порождающей и проверочной матрицами. Для их построения достаточно знать порождающий g(x) и проверочный h(x) многочлены.

Для несистематического циклического кода матрицы строятся циклическим сдвигом порождающего и проверочного многочленов, что эквивалентно умножению этих многочленов на x.

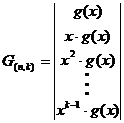и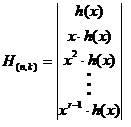

При построении матрицы H_(n,k) старший коэффициент многочлена h(x) располагается справа.

Пример:

Для циклического (7,4) -кода с порождающим многочленом g(x)=x³+x+1 матрицы G_(n,k) и H_(n,k) имеют вид:

 

 

 

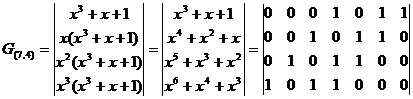
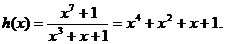
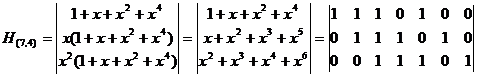
Для систематического циклического кода матрица G_(n,k) определяется выражением:

,

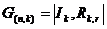где I_k – единичная матрица 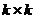, R_k,r – прямоугольная матрица .

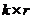Строки матрицы R_k,r определяются из выражения:

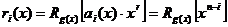
где a_i(x) – полином соответствующий i-той строке матрицы I_k.

Пример:

Матрица G_(n,k) для систематического (7,4) -кода на основе порождающего многочлена g(x)=x³+x+1 строится в следующей последовательности:

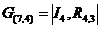
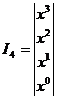
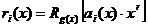
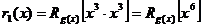
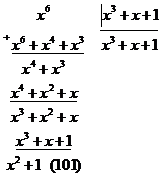или

 

 

 

или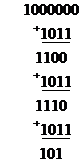

Аналогично определяется:

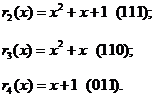
или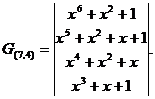

 

Строки матрицы G_(n,k) можно определить непосредственно из выражения:

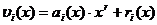
Проверочная матрица в систематическом виде строится на основе матрицы G_(n,k) (также как и для линейных кодов):

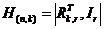
Пример:

Для (7,4) -кода матрица H_(n,k) будет иметь вид:

 

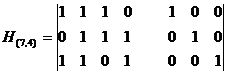
Одна из основных задач, стоящих перед разработчиками устройств защиты от ошибок при передаче дискретных сообщений по каналам связи является выбор порождающего многочлена g(x), который позволит построить циклический код с заданной исправляющей способностью.

У разных классов циклических кодов имеются свои особенности формирования порождающих многочленов g(x).

Важный класс циклических кодов способный исправлять многократные ошибки – БЧХ.

Коды БЧХ

Код БЧХ может быть двоичным и недвоичным. Двоичные БЧХ коды можно построить с параметрами:

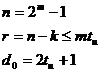
где m>3 – некоторое положительное число, t_и – исправляющая способность кода.

Примитивным кодом БЧХ, исправляющим t_u ошибок, называется код длиной n=q^m-1 над полем GF(q), для которого элементы 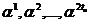являются корнями порождающего многочлена.

Здесь a - примитивный элемент поля GF(q^m), являющегося расширением поля GF(q).

Порождающий многочлен кода БЧХ определяется из выражения:

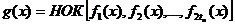
где НОК – наименьшее общее кратное, 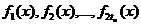- минимальные многочлены корней g(x).

 

Справка: конечные поля.

Код над полем GF(q) имеет основание q. Число q обозначает порядок поля, который равен числу разных элементов содержащихся в этом поле. Порядок конечного поля может быть простым числом q или целой степенью m числа q. Поле GF(q^m) – расширение поля GF(q).

Примитивным элементом a поля GF(q) или его расширения является такой элемент, посредством возведения которого в различные степени можно описать все остальные элементы поля.

Для построения порождающего многочлена кода БЧХ, необходимо выполнить арифметические операции в поле GF(q^m).

Таблицу представления элементов поля рассмотрим на примере поля GF(8)=GF(2³), которое является расширением поля GF(2) по модулю неприводимого многочлена .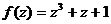

 

Таблица - Таблица элементов поля

Степени примитивного элемента	Многочленные представления	Двоичные представления	Десятичные представления
0	0	000	0
α7=α0=1	1	001	1
α1	z	010	2
α2	z2	100	4
α3	z+1	011	3
α4	z2+z	110	6
α5	z2+z+1	111	7
α6	z2+1	101	5

 

С помощью степенного представления выполняются операции умножения элементов поля. Для выполнения операции сложения необходимо использовать многочленные представления поля.

Конец справки.

 

Минимальный многочлен элемента b поля GF(q^m) определяется из выражения:

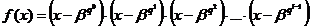
где 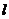- наименьшее целое число, при котором .

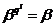Пример:

Определить значение порождающего многочлена g(x) для построения примитивного кода БЧХ над полем GF(2) длины 31, исправляющего двух кратные ошибки (t_u=2).

Исходя из определения кода БЧХ корнями многочлена g(x) являются: 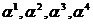, где a - примитивный элемент поля GF(2⁵).

Порождающий многочлен определяется из выражения:

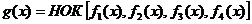
где 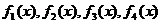- минимальные многочлены корней соответственно .

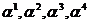Определим 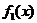. Нужно определить 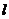- числа сомножителей для выражения .

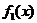В расширении поля GF(2^m) содержится 2⁵=32 разных элементов. 31 из них представляют собой разные степени примитивного элемента a (от нулевой степени до тридцатой). Следовательно, значения a в степени s, при s>30 начнут повторяться:

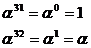
Минимальное число 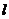, для которого , .

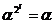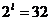Значения минимальных многочленов будут следующими:

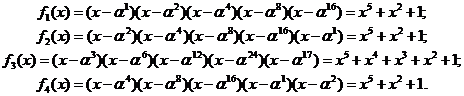
Так как 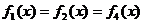, то:

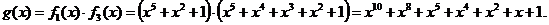
На практике при определении порождающего многочлена используется таблица минимальных многочленов и выражением для порождающего многочлена:

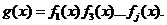
Определение порождающего многочлена осуществляется в следующей последовательности.

По заданной длине кода n и кратности исправляемых ошибок t_u определяют:

1. из выражения n=2^m-1 значение параметра m, который является максимальной степенью сомножителей g(x);

2. из выражения j=2t_u-1 максимальный порядок j минимального многочлена, входящего в число сомножителей g(x);

3. пользуясь таблицей минимальных многочленов, определяется выражение для g(x) в зависимости от m и j. Для этого из колонки, соответствующей параметру m, выбираются многочлены с порядками от 1 до j, которые в результате перемножения дают значение g(x).

Примечание: в выражении для g(x) содержаться минимальные многочлены только для нечетных степеней a, так как обычно соответствующие им минимальные многочлены четных степеней a имеют аналогичные выражения.

Например, минимальные многочлены элементов 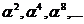соответствуют минимальному многочлену элемента a¹, минимальные многочлены элементов 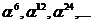соответствуют минимальному многочлену a³ и т.п.

Пример:

Определить значение порождающего многочлена для построения примитивного кода БЧХ над полем GF(2), n=31, t_u=3.

Определяем значения m и j:

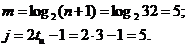
Из таблицы минимальных многочленов в соответствии с m=5 и j=5 получаем:

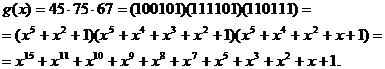
Заданные исходные данные n и t_u или k и t_u для построения циклического кода часто приводят к выбору завышенного значения m и как следствие этого к увеличению длины кода. Такое положение снижает эффективность полученного кода, так как часть информационных разрядов не используется.

 

 

Пример:

Построить циклический код, исправляющий двух кратные ошибки, если длина информационной части кода k=40.

n=2^m-1, ближайшая длина кода равна 63, для которой m=6, а r=mt_u=12. Следовательно, код будет иметь n=63 и k=51. Неиспользованных информационных разрядов будет 51-40=11.

Подобное несоответствие в ряде случаев можно устранить, применяя непримитивный код БЧХ.

Непримитивным кодом БЧХ, исправляющим t_u ошибок, называется код длины n над GF(q), для которого элементы являются 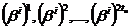корнями порождающего многочлена.

Здесь bⁱ -непримитивный элемент поля GF(q^m), а длина кода n равна порядку элемента bⁱ.

Порядком элемента bⁱ является наименьшее n, для которого .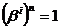

Пример:

Порядок элемента b³ поля GF(2⁶) равен 21, так как .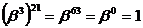

Порождающий многочлен непримитивного кода БЧХ, по аналогии с примитивным кодом, определяется из выражения:

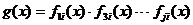
где 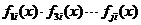- минимальные многочлены элементов 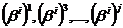поля GF(q^m), которые являются корнями g(x).

Пример:

Определить g(x) для построения непримитивного кода БЧХ над GF(2), n=20, t_u=2.

Из таблицы непримитивных элементов GF(2^m) выбираем поле, элемент b которого имеет порядок больший, но близкий к заданному n. Такими являются GF (2⁶) и b³, порядок которого n=21. Так как j=2t_u-1=3, то выражение для g(x) будет:

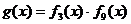
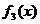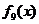где и - минимальные многочлены элементов b³ и b⁹ поля GF(2⁶).

Значения этих многочленов следующие:

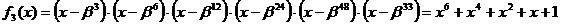
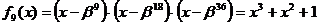
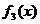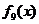Выражения для и можно определить из таблицы минимальных многочленов, используя для этого параметр m поля GF(2^m) и порядковые номера сомножителей g(x).

Для рассмотренного примера m=6, а порядковые номера равны 3 и 9. Поэтому: