2017-12-16
947
1) Произведение любого разрешенного кодового слова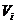 
на транспонированную проверочную матрицу дает нулевой вектор, содержащий 
разрядов.
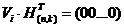
Пример: для кода (6,3)
, 
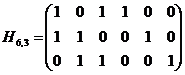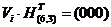
2) Произведение некоторого неразрешенного кодового слова 
на транспонированную проверочную матрицу называется синдромом и обозначается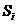 
.
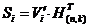
3) Между порождающей и проверочной матрицами в каноническом виде существует соответствие, задающееся равенством:
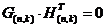
4) Кодовое расстояние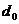 
кода (
, 
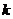) равно минимальному числу линейно независимых столбцов проверочной матрицы. Вычисление 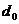по 
осуществляется следующим способом: определяется наличие двух одинаковых столбцов, при обнаружении которых 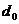= 2. Если их нет, определяется наличие трех столбцов, сумма которых равна нулю, следовательно 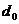= 3. Если 
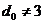, далее последовательно отыскивается 4, 5 и т. д. столбцов, сумма которых равна нулю. При их наличии 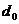= 4, 5 и т. д.
Пример: для кода (5,3)
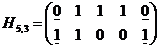следовательно 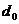= 2.
5) Произведение информационного слова на порождающую матрицу дает разрешенное слово кода.
Пример: для кода (6,3)
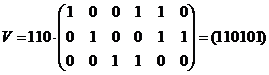
6) Два кода называются эквивалентными, если их порождающие матрицы отличаются перестановкой координат, т.е. порождающая матрица получается в результате перестановки столбцов и перечисленных выше элементарных операций над строками. Эквивалентные коды имеют одинаковые 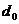и обладают одинаковыми корректирующими свойствами.
7) Кодовое расстояние любого линейного (, 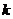)–кода удовлетворяет неравенству (граница Сингтона):
Линейный код, для которого это неравенство превращается в равенство, называется кодом с максимальным расстоянием.
8) Для двоичного линейного (, 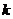)–кода с исправляющей способностью 
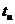= 1, проверочную матрицу модно рассматривать, как таблицу синдромов, при этом синдром определяется по общему правилу свойства (2), а местонахождение ошибки в кодовом слове определяется, как номер столбца в матрице , совпадающего со значением синдрома.
Пример: пусть посредством разработанного кода (6,3) передается информационная комбинация 101. По правилу, изложенному в пункте 5, соответствующая ей разрешенная кодовая комбинация определяется как:
Соответствующая матрица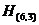 
имеет вид:
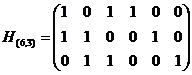
Предположим, что, из-за помех в канале, исказился 3-й слева символ, и была принята неразрешенная комбинация 10 0 011. По правилу свойства 2, соответствующий этой комбинации синдром можно определить как:
совпадает с со столбцом №3 в матрице 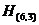, следовательно ошибка в третьем разряде.
