Стандартное расположение группового кода

Стандартное расположение группового кода представляет собой показанное в таблице 2 разложение множества (группы) всех возможных –элементных слов, представляющих собой группу, на смежные классы по подгруппе из 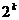кодовых слов, составляющих (, 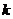)–код, т. е. по подгруппе, включающей в себя все разрешенные комбинации (, 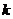)–кода.

Таблица 2

Размешенные в первом столбце кодовые слова называются образующими (лидерами) смежных классов. В стандартном расположении кода они выбираются так, чтобы в их состав входили наиболее вероятные образцы ошибок в кодовом слове.

Пример: код (5,2)

, , а его стандартное расположение имеет вид:

00000 10111 01101 11010 – разрешенные кодовые комбинации

Код (5,2) имеет 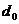= 3. Он гарантирует исправление одиночных ошибок, конфигурация которых дана в первом столбце. Процедура исправления ошибок может быть следующей: Принятое кодовое слово анализируют (путем перебора и сопоставления с ним всех слов, находящихся в таблице стандартного расположения) и определяют, в каком столбце оно находится, а затем, в качестве исправленного кодового слова берут слово, находящееся в верхней строке.

Если длина кода большая и таблица стандартного расположения также большая, пользоваться таким алгоритмом неудобно, поэтому при декодировании используют таблицу синдромов, представляющую собой список образцов ошибок и список соответствующих синдромов, которые однозначно характеризуют каждый смежный класс.

Такую таблицу, например, можно составить на основе проверочной матрицы кода (5,2) . Столбцы этой матрицы совпадают со значениями синдрома, соответствующего наличию ошибки в разряде с номером, равном номеру этого столбца (см. свойство 8). Эта таблица синдромов будет иметь вид:

Значение синдрома	Образец ошибки

Таким образом, с помощью этой таблицы по синдрому можно определить вид лидера смежного класса, совпадающего с образцом ошибки, которому принадлежит принятая комбинация. Для исправления ошибки теперь достаточно сложить (для двоичного кода – по модулю 2) принятую комбинацию с найденным лидером смежного класса.

Коды Хемминга

Коды Хэмминга – класс двоичных блочных кодов, которые имеют следующие параметры:

, (1)

где

Минимальное кодовое расстояние этих кодов 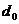= 3, поэтому они способны исправлять все одиночные ошибки или обнаруживать все ошибочные комбинации из двух или менее ошибок в блоке.

Коды Хэмминга являются одним из немногочисленных известных классов совершенных или плотно упакованных кодов, для которых в выражении, определяющем границу Хэмминга, имеет место равенство:

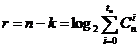, (2)

где

Подставив в выражение (2) 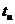= 1 (т. к. код Хэмминга исправляет лишь одиночные ошибки), получаем:

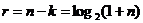
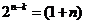(3)

В соответствии с (1), для кода Хэмминга , поэтому равенство (3) очевидно справедливо.

Таким образом, коды Хэмминга имеют наименьшее возможное при заданной длине кодовой комбинации количество проверочных разрядов , которое обеспечивает минимальное кодовое расстояние 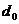= 3, позволяющее гарантированно исправлять все ошибки единичной кратности. При этом, при заданном и одном и том же числе проверочных разрядов, они позволяют максимизировать число .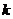

Вычисляя в соответствии с формулой (1), можно получить следующие разряды размерностей кода Хэмминга: (7,4), (15,11), (31,26)…

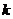С увеличением и , кодовое расстояние 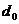, а следовательно, исправляющая способность 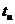не увеличивается, но растет скорость кода .

Проверочная матрица кода Хэмминга имеет строк и столбцов, причем столбцами являются все возможные, отличные друг от друга ненулевые последовательности.

Пример: для кода Хэмминга (7,4)

В канонической форме проверочная матрица выглядит так:

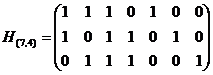, отсюда вытекает следующее правило построения канонической формы поверочной матрицы (, 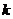)–кода Хэмминга.

Так же, как для любого блочного линейного кода:

, где - единичная матрица, - прямоугольная матрица, столбцами которой являются все возможные разные –разрядные комбинации двоичного кода, не совпадающие с кодовыми словами, имеющими место в столбцах матрицы .

Транспонируя полученную таким образом , можно получить матрицу , а по ней построить порождающую матрицу:

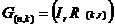
Проверочная матрица любого кода Хэмминга всегда содержит как минимум 3 линейно независимых столбца, поэтому кодовое расстояние всегда равно 3. Если столбцы проверочной матрицы представляют упорядоченную запись десятичных чисел в двоичной форме, то вычисленный синдром однозначно указывает на номер позиции искаженного символа (представляет собой двоичное представление номера искаженного символа).

1 2... 7

Пусть передано кодовое слово 1100110. Предположим, что ошибка в 4 разряде: 110 1 110, тогда:

– код числа 4, следовательно, ошибка в 4 разряде.

Следует отметить, что соответствующий упорядоченной проверочной матрице код является несистематическим. Проверочная матрица в упорядоченном виде позволяет записать совокупность проверочных уравнений, в которых проверочные символы занимают позиции с номерами ,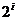

Для кода Хэмминга (7,4):

Первый проверочный символ 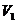занимает позицию в нижней строке матрицы. Местоположение других единиц в этой строке определяет значение индексов слагаемых в правой части первого уравнения. Второй символ занимает позицию во второй строке. Значения индексов слагаемых в правой части второго уравнения определяется положением других единиц в этой строке. Третий символ занимает позицию в четвертой строке матрицы. Значения индексов слагаемых в правой части третьего уравнения определяется положением единиц в этой сроке. При этом элементы синдрома могут быть определены из соотношения:

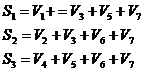
В том случае, если проверочная матрица задана в систематическом виде, синдром определяется по общему правилу: , а местоположение ошибки определяется, как номер столбца в матрице , совпадающего со значением синдрома (см. свойство 8 линейных блочных кодов п. 2.2.2).

Корректирующая способность кода Хэмминга может быть увеличена введением дополнительной проверки на четность. В этом случае проверочная матрица для рассматриваемого кода (7,4) будет иметь вид:

 

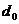, следовательно = 4.

Циклические коды

Основные понятия

Циклическим кодом называется линейный блочный (n,k) -код, для которого циклический сдвиг влево на один разряд любого разрешенного кодового слова дает также разрешенное кодовое слово.

Множество кодовых слов циклического кода может быть представлено совокупностью многочленов степени (n-1) и менее, делящихся на некоторый многочлен g(x) степени r=n-k, являющийся сомножителем двучлена xⁿ+1.

Многочлен g(x) называется порождающим.

Многочленом над полем GF(q) называется математическое выражение вида:

,

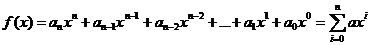где n – длина кода, - коэффициенты из поля GF(q).

Если код построен над полем GF(2), то коэффициенты принимают значения 0 или 1 и код называется двоичным.

Пример: если кодовое слово циклического кода то соответствующий ему многочлен - .

Степень числа x указывает положение соответствующего элемента кодовой комбинации, а коэффициенты многочлена определяют значение этих элементов.

Кодовые комбинации q -ного кода можно интерпретировать многочленом над полем GF(q).

Длина циклического кода называется примитивной и сам код называется примитивным, если его длина n=q^m-1, где m – целое.

Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным.

Как следует из определения общее свойство кодовых слов циклического кода – это их делимость без остатка на некоторый многочлен g(x), называемый порождающим.

Результатом деления двучлена xⁿ+1 на многочлен g(x) является проверочный многочлен h(x):

При декодировании циклических кодов используются многочлен ошибок e(x) и синдромный многочлен S(x).

Многочлен ошибок степени не более (n-1) определяется из выражения:

,

где и - многочлены, отображающие соответственно принятое (с ошибкой) и переданное кодовые слова.

Ненулевые коэффициенты в е(x) занимают позиции, которые соответствуют ошибкам.

Пример:

Синдромный многочлен, используемый при декодировании циклического кода, определяется как остаток от деления принятого кодового слова на порождающий многочлен:

Синдромный многочлен зависит только от многочлена ошибок е(х). Это положение используется при построении таблицы синдромов, применяемой в процессе декодирования. Эта таблица содержит список многочленов ошибок и список соответствующих синдромов, определяемых из выражения:

 

е(х)	S(x)
1	Rg(x)[1]
X	Rg(x)[x]
X2	Rg(x)[x2]
·	·
·	·
·	·
X+1	Rg(x)[x+1]
X2+1	Rg(x)[x2+1]
·	·
·	·
·	·

 

В процессе декодирования по принятому кодовому слову вычисляется синдром S(x), затем в таблице находится соответствующий многочлен е(х), суммирование которого с принятым кодовым словом дает исправленное кодовое слово:

Многочлены можно складывать, умножать и делить, используя известные правила алгебры, но с приведением результата по mod 2, а затем по mod (xⁿ+1), если степень результата превышает степень (n-1).

Пример:

 

 

 

Допустим, что длина кода n=7, то результат приводим по mod (x⁷+1).

 

 

При построении и декодировании циклических кодов в результате деления многочленов обычно необходимо иметь не частное, а остаток от деления. Поэтому рекомендуется более простой способ деления, используя не многочлены, а только их коэффициенты.

Пример: