Способы задания линейных кодов

1) Перечислением кодовых слов

Пример: код (5,3)

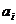– информационные символы

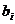– проверочные символы

№ кодового слова	а1	а2	а3	b1	b2

2) Системой проверочных уравнений и табличных уравнений, определяющих правила формирования проверочных символов по известным информационным символам

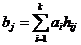, где 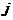– номер проверочного символа, 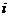– номер информационного символа, 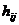– коэффициенты, принимающие значение 0 или 1 в соответствии с правилами формирования конкретного линейного двоичного кода

Пример: для кода (5,3) значение таблицы 1 представлено в матрице коэффициентов.

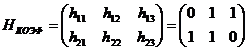при этом:

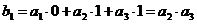
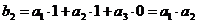
3) Матричный, основанный на построении порождающей и проверочной матриц.

Векторное пространство 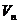над полем GF(2) включает в себя 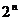векторов ( –последовательностей), а подпространством его множество их 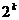кодовых слов длины . Это подпространство однозначно определяется базисом, состоящим из 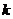линейно независимых векторов. Поэтому линейный (, 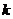)–код можно определить набором из 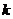линейно независимых кодовых слов, принадлежащих этому коду. Этот набор обычно представляют в виде матрицы, которая называется порождающей. Например, код (5,3) может быть задан матрицей:

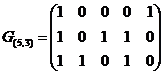
Остальные кодовые слова получаются сложением строк этой матрицы в различных сочетаниях. Можно показать, что общее количество различных вариантов записи порождающей матрицы определяется выражением:

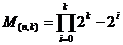
Для исключения неоднозначности в записи 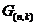вводят понятие канонической или систематической формы матрицы, которая имеет вид:

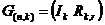, где 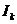– единичная матрица, содержащая информационные символы, 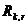– прямоугольная матрица, состоящая из проверочных символов.

Пример: порождающая матрица в каноническом виде для кода (5,3) имеет вид:

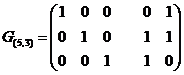
Порождающая матрица 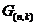в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками:

– Перестановкой двух произвольных строк

– Заменой произвольной строки на сумму ее самой и ряда других

– Дальнейшей перестановкой столбцов

Правило построения проверочной матрицы линейных кодов, обладающих заданной корректирующей способностью 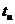или 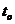, можно сформулировать так:

– Исходя из соотношений, приведенных в пункте 2.1.2 и требований, предъявляемых к исправляющей 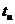или обнаруживающей 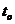способностей кода, определить кодовое расстояние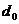

– Исходя из требования числа информационных разрядов, определить необходимые значения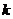

– Строят порождающую матрицу 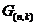в каноническом виде, причем при построении 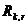руководствуются следующими правилами (данные правила справедливы лишь для двоичных кодов при 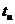= 1, при других значениях 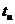процедура является более сложной):

В каждой строке матрицы 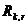должно быть не менее 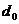–1 единиц. Все 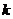строк матрицы 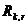должны быть различными, число столбцов должно быть минимальным.

Пример: построить матрицу кода, имеющего 8 информационных комбинаций и исправляющего одиночные ошибки (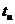 = 1)

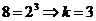
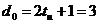
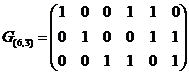
Минимально необходимое число столбцов матрицы в нашем примере равно 3.

Наряду с порождающей матрицей, линейный код может быть задан проверочной матрицей, канонический вид которой выглядит так:

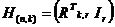
Пример: проверочная матрица, разработанная в предыдущем примере кода (6,3) имеет вид:

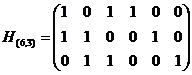
Отметим, что 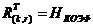(см. второй способ задания кода)