Понятие об оценках параметров генеральной совокупности. Свойства оценок

Пусть неизвестная функция генеральной совокупности зависит от некоторого параметра . Нужно по наблюдениям оценить параметр. Для построения оценок используются статистики – функции от выборочных значений.

Примеры статистик. . Эта оценка .

Будет рассматриваться, как приближенное значение параметра .

Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору , поэтому для установления качества полученных оценок моментов , следует во всех этих формулах заменить конкретные выборочные значения (X_i) на СВ X_i.

; ; .

Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства.

1. Несмещенность, т.е. .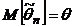

Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной.

Иногда оценка бывает смещенной, но асимптотически несмещенной, т.е. .

2. Состоятельность, т.е. .

Это свойство является обязательным. Несостоятельные оценки не используются.

Эффективность.

а) Если оценки и – несмещенные, то и .

Если , то оценка более эффективна, чем .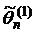

б) Если оценки и – смещенные, тогда и .

Если , то оценка более эффективная, чем .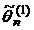

Где – средний квадрат отклонения оценки.