1) Доверительный интервал для оценки МО при известной дисперсии нормально распределенной генеральной совокупности.
Пусть 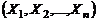 – выборочный вектор n–наблюдений СВ Х, где
– выборочный вектор n–наблюдений СВ Х, где 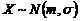 . В качестве оценки для m возьмем
. В качестве оценки для m возьмем 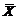 . Предположим, что
. Предположим, что 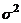 известна. Рассмотрим статистику
известна. Рассмотрим статистику 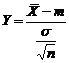 . Статистика
. Статистика 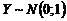 .
.
По таблице нормального распределения найдем квантили 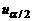 и
и 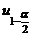 .
.
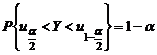 .
.
 .
.
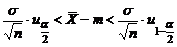 .
.
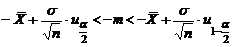 .
.
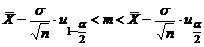 .
.
Учитывая, что 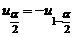 получаем
получаем
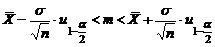 .
.
2) Доверительный интервал для оценки МО при неизвестной дисперсии нормально распределенной генеральной совокупности. Пусть 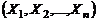 – выборочный вектор n–наблюдений СВ
– выборочный вектор n–наблюдений СВ 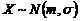 . В качестве оценки для m возьмем
. В качестве оценки для m возьмем 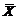 . Если дисперсия генеральной совокупности неизвестна, то по выборке определяем статистику
. Если дисперсия генеральной совокупности неизвестна, то по выборке определяем статистику  . Доверительный интервал для m в этом случае находится с помощью статистики
. Доверительный интервал для m в этом случае находится с помощью статистики 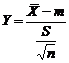 .
.
В литературе по статистике показано, что Y имеет распределение Стьюдента с n–1 степенью свободы 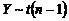 .
.
По заданной доверительной вероятности 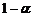 , используя таблицы распределения Стьюдента с n–1 степенью свободы, находим
, используя таблицы распределения Стьюдента с n–1 степенью свободы, находим 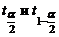 .
.
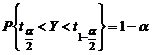 .
.
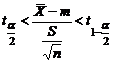 .
.
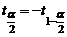
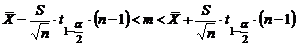 .
.
3) Доверительный интервал для оценки дисперсии при неизвестном МО нормально распределенной генеральной совокупности. Пусть 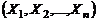 – выборочный вектор n–наблюдений СВ
– выборочный вектор n–наблюдений СВ 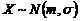 . В этом случае в качестве оценки дисперсии
. В этом случае в качестве оценки дисперсии 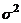 используют
используют 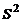 .
.
В литературе по математической статистике доказано, что 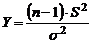 имеет распределение
имеет распределение 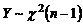 .
.
По таблице распределения 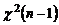 определяются квантили
определяются квантили 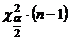 и
и 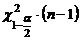 .
.
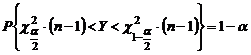
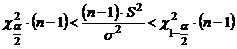
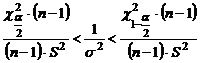 .
.
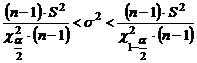 .
.
 2017-12-16
2017-12-16 441
441








