Каждому значению х числовой прямой поставим в соответствие долю членов совокупности, у которой изучаемый признак имеет значение <x и обозначим ее  . С изменением х, вообще говоря, меняется и
. С изменением х, вообще говоря, меняется и  , т.е.
, т.е.  есть функция от х.
есть функция от х.
Эмпирической функцией распределения совокупности по признаку А называется функция  , выражающая для каждого х долю тех ее членов, у которых признак А имеет значение <х.
, выражающая для каждого х долю тех ее членов, у которых признак А имеет значение <х.
Если число таких членов m(x), а объем совокупности n, то:

Пусть имеется некоторая ген. совокупность, каждый объект которой наделен количественным признаком Х. При случайном извлечении объекта из ген. совокупности становится известным значение х признака Х этого объекта.
Т.о., мы можем рассматривать извлечение объекта из ген. совокупности, как испытание; Х, как СВ; х, как одно из возможных значений Х.
Опытные значения признака Х можно рассматривать как значения разных СВ  ,
,  , …
, …  с тем же распределением, что и Х. И, следовательно, с теми же числовыми характеристиками, которые имеет Х. Значит,
с тем же распределением, что и Х. И, следовательно, с теми же числовыми характеристиками, которые имеет Х. Значит,  и
и 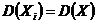 .
.
Величины  ,
,  , …
, …  можно считать независимыми в силу независимости наблюдений. Значения
можно считать независимыми в силу независимости наблюдений. Значения  ,
,  , …
, …  в этом случае называются реализациями СВ
в этом случае называются реализациями СВ  ,
,  , …
, … 
 2017-12-16
2017-12-16 1135
1135








