Уравнения первого порядка с разделяющимися переменными

Определение 4.2.1. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно имеет вид:

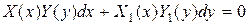
где – функции только переменной х, а – функции только переменной у.

Для решения уравнения (4.2.3) разделим обе его части на произведение 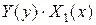, предполагая, что оно не равно нулю, тогда получим

В уравнении (4.2.4) при dx стоит функция только от х, а при dy – только от у. В этом случае говорят, что переменные разделены.

Беря интегралы от левой и правой частей равенства (4.2.4), получаем:

Здесь под интегралами понимаются некоторые соответствующие первообразные.

Соотношение (4.2.5) и представляет собой общее решение уравнения (4.2.3).

Кроме того, решениями уравнения (4.2.3) могут быть корни уравнения , откуда

или ,

или – также решения уравнения (4.2.3).

Пример 4.2.1. Решить уравнение .

○Из уравнения получим xdy = ydx, х ¹0.

Пусть y ¹0, тогда разделим обе части уравнения на хy ¹0, получим:

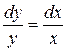(разделили переменные).

Интегрируя последнее равенство, получим:

, откуда

.

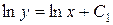Положим , тогда

,

,

.

Решим уравнение хy =0. Так как х ¹0, то у =0. Так как у =0 получается из решения при С=0, то решением данного уравнения является . ●