Случаи понижения порядка дифференциальных уравнений

(4.3.6)

Укажем два случая, когда дифференциальное уравнение второго порядка

приводится к дифференциальному уравнению первого порядка.

(4.3.7)

Случай 1. Пусть правая часть дифференциального уравнения (4.3.6) явно не содержит х, т.е. уравнение имеет вид

.

Полагая здесь

,

где p – функция от y, получим дифференциальное уравнение первого порядка

,

где роль независимой переменной играет y.

Случай 2. Пусть правая часть дифференциального уравнения (4.3.6), явно не содержит у, т.е. уравнение имеет вид

(4.3.8)

.

Полагая

и ,

получим уравнение первого порядка

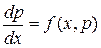
с неизвестной функцией р.

Пример 4.3.1. Решить уравнение

(4.3.9)

.

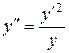○ Согласно случаю 1 полагаем и . Тогда уравнение (4.3.9) примет вид

.

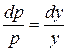Отсюда: 1) p =0, т.е. у =С; или 2) , т.е. и

.

Потенцируя, будем иметь

, т.к. , то .

После интегрирования получаем

,

и, значит,

,

,

где и – произвольные постоянные.●

Пример 4.3.2. Найти решение уравнения

(4.3.10)

,

удовлетворяющее начальным условиям: и при .

○В уравнении (4.3.10) полагаем и . Тогда

,

или

(4.3.11)

.

Полученное уравнение – однородное[1], поэтому примем , .

Подставляя в уравнение (4.3.11), будем иметь

,

,

,

.

Интегрируя, получаем

и, следовательно, , т.е. и .

Для определения постоянной используем начальные условия: при . Получаем , т.е. =0 и, т.о.,

.

Отсюда имеем и

(4.3.12)

.

Постоянную определяем из начальных условий. Полагая и в формуле (4.3.12), получаем 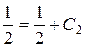, т.е. =0. Следовательно, искомое частное решение есть . ●