2017-10-31
388
|
имеет постоянные коэффициенты 
и 
.
|
,
где k – постоянное число, подлежащее определению. Из (4.3.18) имеем
и 
.
Подставляя 
, 
и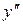 
в уравнение (4.3.17), получаем
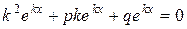
или, сокращая на множитель 
, который не равен нулю, находим
|
.
Квадратное уравнение (4.3.19), из которого определяется число k, называется характеристическим уравнением данного линейного уравнения второго порядка с постоянными коэффициентами (4.3.17). Заметим, что для написания характеристического уравнения (4.3.19) достаточно в дифференциальном уравнении (4.3.17) производные 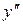, и функцию y заменить на соответствующие степени величины k, рассматривая при этом функцию y как производную нулевого порядка.
Решая характеристическое уравнение (4.3.19), получаем
|
.
Здесь могут представиться три различных случая.
Случай 1. Если
|
,
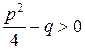то, согласно формуле (4.3.20) характеристическое уравнение (4.3.19) имеет два различных действительных корня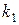 
и 
. Следовательно, линейное уравнение (4.3.17) допускает два различных частных решения
и 
.
Так как 
, то эти решения линейно независимы. Следовательно, общее решение для случая 1 имеет вид
|
.
|
.
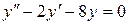Решая характеристическое уравнение
,
находим его корни 
, 
. Общее решение уравнения (4.3.23) имеет вид
.
Случай 2. Если
,
то в силу формулы (4.3.20) характеристическое уравнение (4.3.19) имеет единственный корень
.
Такой корень называется кратным. Поэтому одно частное решение уравнения (4.3.17) будет
.
Всякое другое частное решение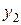 
, линейно независимое с 
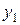, будет иметь вид
|
.
Таким образом, общее решение уравнения (4.3.17) в случае 2 будет
|
.
Пример 4.3.4. Пусть
.
Решая характеристическое уравнение 
, находим кратный корень 
. Следовательно, общее решение запишется в виде 
.
Случай 3. Если
рассматривать не будем [2].
