2017-10-31
409
Рассмотрим линейное неоднородное уравнение второго порядка
|
,
где p и q – данные постоянные числа, f(x) (правая часть уравнения) – известная функция от x. Имеет место следующая теорема.
Теорема 4.3.2. Общее решение неоднородного уравнения (4.3.26) равно сумме общего решения соответствующего однородного уравнения
|
и частного решения данного неоднородного уравнения.
Для нахождения частного решения уравнения (4.3.26) обычно применяется так называемый метод неопределенных коэффициентов.
Случай 1. Правая часть уравнения (4.3.26) есть показательная функция
.
Ищем частное решение z также в форме показательной функции
|
,
где А – неопределенный коэффициент. Отсюда
и 
.
Подставляя f(x) и выражения для z и его производных в уравнение (4.3.26), после сокращения на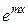 
будем иметь
|
.
Возможны два случая:
1) m не является корнем характеристического уравнения, т.е.
.
Тогда 
и, следовательно,
;
2)
|
.
Тогда уравнение (4.3.29) противоречиво и, следовательно, дифференциальное уравнение (4.3.26) не имеет частного решения в форме (4.3.28).
В этом случае:
а) если m есть простой корень характеристического уравнения (т.е. другой корень этого уравнения отличен от m), то частное решение уравнения (4.3.26) следует брать в виде
;
б) если же m – кратный корень характеристического уравнения, то частное решение уравнения (4.3.26) нужно искать в виде
Пример 4.3.5. Пусть 
.
Решим сначала уравнение без правой части:
.
Характеристическое уравнение здесь имеет вид 
. Отсюда корни его будут 
, 
. Следовательно, общее решение уравнения без правой части таково:
.
Так как m =1 не является корнем характеристического уравнения, то ищем частное решение уравнения с правой частью в следующей форме:
,
где А – неопределенный коэффициент. Дифференцируя будем иметь
, 
.
Подставляя эти выражения в наше неоднородное уравнение, получаем
или 
.
Отсюда 
. Итак, частное решение уравнения с правой частью есть
.
Общее же решение этого уравнения на основании предыдущей теоремы имеет вид
.
|
.
Ищем частное решение z этого уравнения также в форме тригонометрического полинома
,
где А и В – неопределенные коэффициенты.
Дифференцируя, получим
и 
.
Отсюда, подставляя эти выражения в уравнение (4.3.26) и собирая вместе члены с 
и 
, будем иметь
Так как последнее равенство представляет собой тождество, то коэффициенты при и в левой и правой частях этого равенства должны быть соответственно равны друг другу. Получим
, 
.
Из этой системы, вообще говоря, мы и сможем определить коэффициенты А и В. Единственный случай, когда система несовместна, это
.
Тогда частное решение z следует брать в такой форме:
.
Пример 4.3.6. Пусть
|
|
Решая характеристическое уравнение 
, находим кратный корень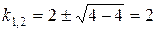 
.
Следовательно, общее решение однородного уравнения (4.3.33) есть
.
Будем искать частное решение уравнения (4.3.32) в форме
,
где А и В – неопределенные коэффициенты.
Дифференцируя, получаем
, 
.
Подставляя 
, 
, 
в уравнение (4.3.32), будем иметь
.
Приравнивая коэффициенты при 
и 
справа и слева, получим систему
решая которую, получим 
и, следовательно,
.
Отсюда общее решение уравнения (4.3.32) будет иметь вид
.
Случай 3. Правая часть линейного уравнения (4.3.26) представляет собой полином, например, второй степени
|
.
Ищем частное решение z этого уравнения также в форме полинома второй степени
где А, В, С – неопределенные коэффициенты.
Дифференцируя, будем иметь
и 
.
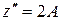Отсюда, подставляя , , в уравнение (4.3.26), получаем
,
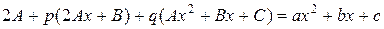или
.
Так как два многочлена тождественно равны друг другу тогда и только тогда, когда коэффициенты при одинаковых степенях переменной х равны, то для определения коэффициентов А, В и С имеем систему
|
Если 
, то из этой системы для коэффициентов А, В, С получаются определенные числовые значения. Тем самым частное решение z будет вполне определено.
Если же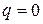 
(характеристическое уравнение имеет простой нулевой корень), то система (4.3.35) несовместна. В этом случае, полагая, что 
, частное решение z следует искать в форме
.
Аналогично нужно поступать, если f (x) есть полином какой-нибудь другой степени.
Пример 4.3.7. Найти решение 
уравнения
|
,
такое, что
|
.
Однородное уравнение здесь следующее:
.
Характеристическое уравнение 
имеет корни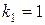 
, 
. Следовательно, общее решение однородного уравнения есть
,
где 
и 
– постоянные.
Для нахождения частного решения z неоднородного уравнения (4.3.36) полагаем
.
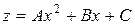Подставляя эту функцию в уравнение (4.3.36), будем иметь
.
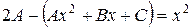Отсюда
следовательно, А =–1, В =0, С =–2 и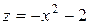 
.
Общее решение неоднородного уравнения (4.3.36) имеет вид
|
.
Дифференцируя, находим
|
.
Полагая х =0 в формулах (4.3.38) и (4.3.39) и используя начальные условия (4.3.37) получаем систему
Таким образом, 
.
Подставляя эти значения в формулу (4.3.38), получаем искомое решение
.
[1] Уравнение (4.3.11) можно также рассматривать как линейное
[2] Познакомиться с решением уравнения (4.3.17) в случае 3 можно, например, в книге: Краткий курс высшей математики / Б.П. Демидович, В.А. Кудрявцев. – М.: ООО «Издательство Астрель»; ООО «Издательство АСТ», 2003. – С. 480.
