Решение дифференциальных уравнений

Дифференциальное уравнение–уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные. Порядок или степень дифференциального уравненияопределяется наибольшимпорядком производной, входящей в это уравнение.Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – уравнением в частных производных.

Примерамизаписи дифференциальных уравнений могут служить следующие уравнения:

В общем случае решение дифференциального уравнения n-го порядказаключается в отыскании функции x=x(t), при подстановке которой в уравнение (1),последнее обращается в тождество:

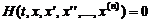(1)

Каждое дифференциальное уравнение имеет бесчисленное множество решений, которые отличаются друг от друга константами. Для однозначного определения решения требуется задать дополнительные начальные или граничные условия. Количество таких условий должно совпадать с порядком дифференциального уравнения или системы. В зависимости от вида дополнительных условий в дифференциальных уравнениях различают:

1) задачу Коши – все дополнительные условия заданы в одной точке интервала;

2) краевую задачу – дополнительные условия указаны на границах интервала.

Для дифференциального уравнения n -го порядка задача Коши состоит в нахождении решения x=x(t), удовлетворяющего уравнению (1) и начальным условиям (2).

(2)

Уравнение (1) сводится к системе n обыкновенных дифференциальных уравнений первого порядка заменой на неизвестную функцию p. Например, уравнение второго порядка можно записать в виде системы двух уравнений:

Различают точные (аналитические) и приближенные (численные) методы решения дифференциальных уравнений. К аналитическим методам относятся метод последовательного дифференцирования, использующий разложение в ряд Тейлора, и метод последовательных приближений.

В системе MATLAB для аналитического (символьного) решения дифференциальных уравнений или систем дифференциальных уравнений используется функция dsolve, имеющая следующий синтаксис:

dsolve(‘expr1’, ‘expr2’,…, ‘exprn’, ‘cond1’,‘cond2’,…, ‘condn’, ‘var’)

где: expr1, expr2,…, exprn –символьная запись дифференциальных уравнений, cond1, cond2,…, condn –граничные условия, var – независимая переменная, опциональный параметр, по умолчанию независимой переменной считается переменная t.

Имя независимой переменной не должна начинаться с D, так как это символ обозначает производную по независимой переменной: D=d/dt, D2=d²/dt².

Пример: необходимо найти аналитическое решение следующего дифференциального уравнения:

Для нахождения решения данного дифференциального уравнения в системе MATLABнеобходимо выполнить следующую команду:

>>dsolve(‘Dx*t*(1+t^2)=x+x*t^2–t^2’, ‘x(0)=–pi/4’);

Однако, существуют дифференциальные уравнения, не имеющие аналитического решения, поэтому широкое распространение получили численные методы решения обыкновенных дифференциальных уравнений. К наиболее распространенным методам численного решения дифференциальных уравнений относят метод Эйлера, усовершенствованный метод Эйлера (Метод Эйлера – Коши), методы Рунге-Кутты, метод прогноза-коррекции Адамса.

Суть численных методов решения дифференциальных уравнений рассмотрим для следующего примера. Пусть требуется найти решение задачи Коши для дифференциального уравнения первого порядка, удовлетворяющего начальному условию:

Иными словами, требуется найти интегральную кривую x=x(t), проходящую через точку M₀(t₀, x₀).

 

Метод Эйлера

Для решения задачи Коши выберем достаточно малый шаг h и построим на интервале [t₀; t_n] систему равноотстоящих точек:

В этом случае можем записать:

(3)

Процесс нахождения значения функции xiв узловых точках tiпо формуле (3) называется методом Эйлера. Основным недостатком этого метода является его невысокая точность.