Модифицированный метод Эйлера

Более точным методом решения дифференциальных уравнений является модифицированный метод Эйлера, при котором сначала вычисляют промежуточные значения:

Далее находят значения x_i₊₁ по формуле:

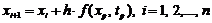
Метод Рунге – Кутты

Рассмотренные методы Эйлера являются частными случаями методов Рунге-Кутты k -го порядка. В общем случае формула вычисления очередного приближения методом Рунге-Кутты имеет вид:

Функция φ(x, t, h) аппроксимирует отрезок ряда Тейлора до k -го порядка и не содержит частных производных f(t, x).

Метод Эйлера является методом Рунге-Кутты первого порядка (k =1) и получается при φ(x, t, h)= f(t, x).

Семейство методов Рунге-Кутты второго порядка имеет вид:

Модифицированный метод Эйлера является частным случаем метода Рунге-Кутты второго порядка при a =1.

Наиболее распространенными методом численного решения дифференциальных уравнений является метод Рунге-Кутты 4-го порядка, расчетные формулы которого можно записать в виде:

Система MATLAB позволяет решать дифференциальные уравнения и системы высокого порядка с табличным и графическим представлением результатов.В среде MATLABдля нахождения численного решения дифференциальных уравнений используются встроенные функции семейства ode (), реализующих методы Рунге-Кутты различных порядков. Функции ode23 () реализует численные методы Рунге-Куттавторого порядка, функция ode45 () – четвертого порядка. Обе функции имеют одинаковый синтаксис следующеговида:

[t, x]=ode45(‘fun’, [t₀t_f], x₀, tol, trace)

где: 'fun' – имя m-файла, в котором содержатся правые части системы дифференциальных уравнений, t₀ – начальное значение аргумента, t_f – конечное значение аргумента, x₀ – вектор начальных условий, tol – задаваемая точность, опциональный параметр, по умолчанию равен для ode23() – 10^-З, для ode45() – l0^-6, trace –опциональный параметр, обеспечиваетотображение промежуточных результатов.

Алгоритм решения дифференциальных уравнений в системе MATLAB включает в себя два этапа: создание новой файл-функциив виде m-файла в среде MATLABдля вычисления правой части дифференциального уравнения и использованиеодной из функции ode () для непосредственногополучения решения.

Пример: найти решение задачи Коши для следующего дифференциального уравнения:

1. Создаем файл-функцию и сохраняем ее в виде m-файла с произвольным именем:

function f=eq1(t,x)

f= –x+sin(x*t)

end

2. Используем одну из функций ode (), выберем интервал интегрирования уравнения[0, 35]; вызовем функцию ode45 для использования метода Рунге-Кутты четвертого порядка для нахождения численного решения уравнения:

[t,x] = ode45(@eq1, [0 35], 1,5)

В данном случае @eq1 это ссылка на созданнуюm-файл, содержащий функцию f(x,t), т.е. правую часть дифференциального уравнения, другой формой вызова файл-функции является обращение к ней следующим образом: ‘eq1’. Для графической иллюстрации найденного решения необходимо построить график зависимости x=x(t) с помощью функции plot(t, x). Результатом решения дифференциального уравнения является график зависимости, приведенный на рисунке 1.