Основні теоретичні положення. Процедура знаходження проміжних значень функції між заданими n точками називається інтерполяцією

Процедура знаходження проміжних значень функції між заданими n точками називається інтерполяцією.

Відповідно, задані в n окремих точках значення функції, називаються вузлами інтерполяції. Геометрично задача інтерполювання для функції однієї змінної y = f(x) означає побудову кривої, що проходить через відомі точки з координатами (x₁, y₁), (x₂, y₂),...(x_n, y_n),де x_1..., x_n — вузли інтерполяції, y_1,,y_n— значення функції y(x) в цих точках. В методах інтерполяції для представлення невідомої функції y(x) може бути обраний поліном P(x) степені n-1, такий, що Р(х) наближено виражає функцію y(x):

 

(7.1)

 

(7.2)

 

Коефіцієнти а_n,...а₀ для інтерполювання заданої функції y(x) визначаються із умови, що Р(х₀) = у₀, Р(х₁) = у₁, Р(х_n) = у_n . Інтерполяція поліномом Лагранжа L(x) при довільному розташуванні вузлів в загальному випадку зводиться до обчислення у(х) = L(х) за допомогою інтерполяційного полінома:

Екстраполяція — отримання значень f(x) при х, що не належить відрізку [ a, b ], на якому задана функція. Вона також здійснюється за формулами інтерполяції, але із значно більшою похибкою. Для плавних f(x) екстраполяція доцільна при х, що виходить за вказані межі не більше, ніж на половину кроку сітки. У MathCad існує функція predict(y,m,n) – для передбачення вектора, що екстраполює вибірку даних, де у - вектор дійсних значень, через рівні проміжки значень аргументу; m - кількість послідовних елементів вектора у, по яким будується екстраполяція; n - кількість елементів вектора передбачень.

Обернена інтерполяція — процес знаходження значень х по заданих значеннях у. Для монотонних функцій між прямим та оберненим інтерполюванням не має різниці. Єдина відміна полягає в тому, що обернена таблиця значень х(у) буде мати змінний крок, навіть якщо пряма таблиця мала постійний. Але формули інтерполювання розраховані на змінний крок.

Пакет MathCad пропонує для лінійної інтерполяції функцію linterp(Х,Y,xp), (xp — довільна координата, або масив точок вектора X), функція здійснює лінійну інтерполяцію на основі векторів значень Х та Y. Лінійна інтерполяція полягає в визначенні прямих ліній залежності Y(Х) між точками даних, на основі яких обчислюються інтерпольовані значення.

Багатоінтервальна інтерполяція полягає в інтерполяції f(x) в ряді часткових інтервалів (обмежених двома вузлами або групою вузлів) окремими поліномами невисокого степеня. Сплайн-інтерполяція є спеціальною різновидністю багатоінтервальної інтерполяції, при якій поліном, що інтерполює забезпечує не тільки рівність g(x) = у_і у вузлах інтерполяції, але й неперервність заданої кількості перших похідних на границях часткових інтервалів. Математично сплайн це спеціальний многочлен, який приймає у вузлах значення g(x) = y_i = y(x_i) і забезпечує в них неперервність першої та другої похідних.

Для сплайн-інтерполяції пакет підтримує чотири вбудованих функції: lspline, pspline, cspline та interp. Сплайн-інтерполяція реалізується у два етапи:

- на першому етапі використовується одна з функцій, яка формує вектор других похідних S:=lspline(X,Y) або функції: pspline, cspline. Три вказані функції відповідають трьом різним типам кривих, які використовуються для інтерполяції на відрізках між двома сусідніми точками Х — пряма лінія, парабола, кубічна парабола;

- на другому етапі використовується функція interp(S,X,Y,xp), аргументами якої є чотири значення: вектор S других похідних, вектори даних Х, Y та координата xp точки інтерполяції. Кубічна сплайн-інтерполяція відповідає з’єднанню заданих пар точок [ X_i, Y(X_i) ] та [ X_i+1, Y(X_i+1) ] плавною кривою, тип якої визначається згідно функції, обраної на першому етапі інтерполяції.

Отже, інтерполяція дозволяє достатньо просто апроксимувати емпіричні залежності. Однак точність такої апроксимації гарантована лише в обмеженому інтервалі декількох кроків при рівномірній сітці, а при нерівномірній — лише в малому околі вузла інтерполяції. При інтерполяції ми прирівнюємо значення P(x) та у(х) у вузлах. Якщо у(х_і) визначені не точно, обтяжені похибками, то точне прирівнювання недоцільне. В подібних випадках краще наближати функцію не по точках, а в середньому. Таке наближення називається середньоквадратичним, а метод, за яким визначаються параметри апроксимуючої функції, називається методом найменших квадратів (МНК).

При експериментальному вивченні функціональної залежності однієї величини Y від іншої величини Х виконують ряд вимірювань величини Y при різних значеннях величини Х. Задача обробки полягає в аналітичному представленні шуканої функціональної залежності, тобто в підборі формули, що описує результати експерименту. Особливість цієї задачі в тому, що наявність випадкових помилок вимірювань робить недоцільним підбір такої формули, яка б точно описувала усі дослідні значення.

Емпіричну формулу, зазвичай, вибирають із формул визначеного типу, наприклад, y = ax + b, y = a^ebx + c, y = a + hsin(ωx + φ). Вибір того чи іншого типу формул обумовлений, в першу чергу, фізичною природою даних, що вивчаються, наявною апріорною інформацією про характер їхньої залежності та іншими факторами, зокрема простотою аналітичного представлення емпіричного матеріалу.

Математична суть даної задачі — визначення параметрів a, b, c,... обраної формули. Позначимо обрану функціональну залежність як y = f(x; a₀, a₁,..., a_n). Параметри a₀, a₁,..., a_n потрібно визначити. Але це неможливо зробити точно за значеннями функції y₁, y₂,..., y_n, оскільки вони містять випадкові величини. Мова йде лише про найкраще наближення функції вихідних даних. Таке наближення здійснюється методом найменших квадратів (МНК), суть якого полягає в наступному: якщо усі виміри значень функції y₁, y₂,..., y_n виконані з однаковою похибкою, то оцінки параметрів a₀, a₁,..., a_n визначаються з умови, щоби сума квадратів різниці виміряних значень у_k найменше відрізнялась від розрахункових f(x; a₀, a₁,..., a_n), тобтовеличина приймала найменше значення.

 

(7.3)

Визначення тих значень параметрів a₀, a₁,..., a_n, які приймають найменше значення функції

S = S(a₀, a₁,..., a_n) зводиться до розв'язку системи рівнянь

(7.4)

Залежність виду y = ax + b — це лінійна функція, що графічно зображується прямою лінією. Така залежність широко використовується при обчисленні значень одного фізичного параметра по відомим значеннями іншого.

При визначенні параметрів a, b лінійної функції y = ax + b за МНК система рівнянь (8.4) зводиться до виду

(7.5)

Розв'язок цієї системи дає формули для коефіцієнтів a, b

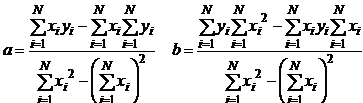(7.6)

 

В пакеті MathCad лінійна апроксимація за МНК здійснюється двома вбудованими функціями а:=slope(X,Y) та b:=intercept(X,Y). Аргументами цих функцій є вектори даних X,Y. Рівняння апроксимуючої прямої з використанням цих функцій записується формулою

P = xp · slope(X,Y) + intercept(X,Y), (7.7)

де xp — довільна координата X. Елементи вектора X повинні йти в порядку зростання значень; Y є дійсний вектор однієї розмірності з X.

Пакет підтримує ще одну групу функцій, що здійснюють апроксимацію одно- та багатовимірних даних за МНК.

Одновимірна апроксимація поліномом n -го степеня здійснюється у два етапи:

¾ використовується функція regress(X,Y,n), що повертає вектор значень, потрібний для наступної функції interp, у цій функції(n - степінь полінома);

¾ використовується функція interp(S,X,Y,xp), що повертає оцінку значення Y, яка відповідає X, де X, Y — вектори даних; S — вектор значень, що повертає функція regress.

Для великих наборів даних, коли залежність Y від X в різних частинах масиву суттєво змінюється, доцільно використовувати для апроксимації не один поліном, а сукупність поліномів. Для цього в пакеті є функція loess(X,Y,span), яка повертає вектор значень, потрібний функціїї interp щоб знайти сукупність поліномів другого порядку, яка найкраще наближує дані X та Y. Аргумент span визначає, наскільки великі набори даних будуть наближатися окремими поліномами. Звичайно апроксимацію даних виконують при n < 5, span = 0.4 - 0.75.

Згладжування — це процедура осереднення експериментальних даних з метою зменшення впливу випадкових похибок і встановлення характеру залежності. Згладжування емпіричних даних подібне до процесів інтерполяції та апроксимації.

Згладжування, зокрема, виконується за допомогою поліномів, які наближають за МНК обрані групи експериментальних даних. Оскільки найкращі результати отримують для середньої точки групи даних (коли враховується інформація про поведінку функції по обидві сторони від точки, в якій проводиться згладжування), то кількість точок для цього обирається непарною, а група точок в процесі згладжування "ковзає" вздовж вхідних даних. Значення побудованого таким чином полінома в точці x_i є згладженим значенням функції в точці x_i пересувається на один крок і процес повторюється, поступово згладжуючи всю функцію. Такий метод називається методом рухомої смуги або ковзаючого вікна.

На практиці вибір тієї чи іншої формули визначається, звичайно, неформальним шляхом. Вказаний метод згладжування має певні недоліки — досить часто не співпадають місця знаходження великих екстремумів до і після згладжування; відсутність згладжених значень на кінцях залежності. Усі способи згладжування потрібно застосовувати обережно, оскільки при цьому можна до певної міри спотворити дійсну поведінку функції і тим самим втратити корисну інформацію.

Ця процедура реалізована в пакеті функцією, яка виконує згладжування даних у "ковзаючому вікні" заданої ширини. Функція називається medsmooth(Y, n). Аргументи даної функції: Y — вектор із m елементів; n — ширина "вікна", в якому відбувається згладжування. При цьому n повинно бути непарним числом, меншим за кількість елементів m. Функція повертає вектор, якій складається із m елементів.

Є ще дві вбудовані функції, призначені для виконання операцій згладжування різними методами:.

- функція ksmooth(X,Y,b) — повертає вектор з n згладжених елементів, які розраховуються використовуючи Гаусове ядро для розрахунку локальної ваги елементів-складників вектора Y. Для кожного елемента ksmooth -функція повертає новий елемент Y. Аргументи даної функції: X — вектор аргументів згладжуваної функції із n елементів; Y — вектор дійсних значень функції із n елементів; b — ширина вікна згладжування. Величина b звичайно встановлюється у декілька разів більше інтервалу між значеннями X. Для цього необхідно обчислити середню відстань між точками X:

(7.8)

- функція supsmooth(X,Y) — повертає вектор з n згладжених елементів, які обчислюють на основі використання процедури лінійного згладжування по МНК за правилом k - найближчих сусідів з адаптивним вибором k Гауса. Цю функцію доцільно використовувати, якщо дані (значення Y) знаходяться у смузі відповідно постійної ширини.