2018-01-08
643
Лабораторная работа №1
Решение экономических задач с помощью методов теории линейного программирования и использования ЭВМ
Цель: научиться строить математические модели экономических задач в форме задач линейного программирования и решать их с помощью ЭВМ.
Задание: записать задачи об оптимальном ассортименте выпускаемой продукции и о смесях в форме задач линейного программирования и решить их с помощью ЭВМ.
Краткие теоретические положения
Задача об определении оптимального ассортимента
Имеется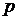 
видов ресурсов в количествах 
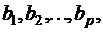, которые могут быть использованы при производстве 
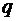видов изделий. Заданы:
1) технологическая матрица производства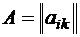 
, где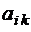 
характеризует нормы расхода 
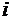-го ресурса на единицу 
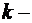го изделия, 
;
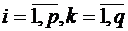2) прибыль от реализации 1 ед. продукции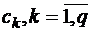 
(эффективность производства 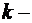го изделия).
Требуется определить план выпуска изделий (оптимальный ассортимент), при котором прибыль максимальна.
Пусть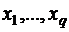 
- объёмы производства, тогда математическая модель задачи имеет вид:
|
|
|
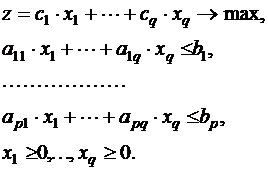(1)
где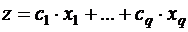 
- суммарная величина прибыли, 
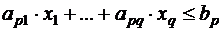- ограничение на запас 
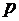-го ресурса.
Задача (1) является задачей ЛП. Решив её с помощью симплекс-метода, получим оптимальный план работы предприятия, как набор величин вида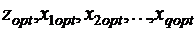 
.
Задача о смесях
Имеется 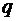компонентов, при сочетании которых в различных пропорциях образуются различные смеси. В состав каждого компонента входят 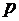питательных веществ. Известны:
1) содержание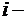 
го питательного вещества, которое входит в единицу 
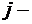го компонента 
, 
, 
;
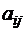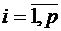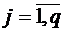2) закупочные цены единицы каждого компонента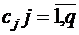 
;
3) минимально необходимое содержание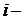 
го вещества в смеси 
.
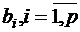Требуется определить состав смеси, т.е. числа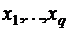 
, который имеет наименьшую стоимость и при этом в смеси должны содержаться питательных веществ в объёме не меньшем, чем нормы потребления. Для решения данной задачи записываем математическую модель в форме задачи линейного программирования вида:
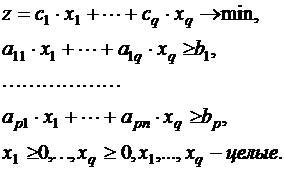(2)
Индивидуальное задание
Задача 1. Мебельная фабрика может выпускать столы, стулья, бюро и книжные шкафы. При изготовлении этих товаров используются два вида досок, имеющихся в количестве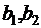 
м. соответственно и трудовые ресурсы в объеме 
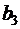чел./ч. Известна прибыль от реализации 1 ед. каждого изделия, равная 
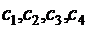руб./шт. Нормативы затрат каждого из видов ресурсов на 1 ед. изделия приведены в таблице:
Таблица 1.
| Ресурсы\ Изделия | Столы | Стулья | Бюро | Шкафы |
| Доски 1 типа (м) | ||||
| Доски 2 типа (м) | ||||
| Трудовые ресурсы (чел./ч.) |
Числовые параметры задачи, в зависимости от номера варианта Nv, приведены в таблице 1 приложений.
|
|
|
Требуется:
а) Составить по значениям параметров задачу ЛП с числовыми коэффициентами, решить ее с помощью ЭВМ и определить оптимальный ассортимент выпуска продукции.
б) Решить ту же задачу при дополнительных условиях, налагаемых на ассортимент: столов - не менее 40, стульев не менее 100, бюро не менее 30 и книжных шкафов не более 8, количество столов относится к количеству стульев, как 1:6.
Задача2. В состав рациона кормления могут входить три продукта: сено, силос и концентраты, содержащие питательные вещества: белок, кальций и витамины. Содержание питательных веществ (в г на 1 кг.), минимально необходимые нормы их потребления и цены закупки 1кг продукта задаются таблицей:
Таблица 2.
| Продукты \ Пит. В-ва | Цена р./кг | Белок | Кальций | Витамины |
| Сено | 0.5 | а11 | а21 | а31 |
| Силос | а12 | а22 | а32 | |
| Концентраты | а13 | а23 | а33 | |
| Нормы потребления |
Числовые значения параметров находятся, в зависимости от номера варианта Nv, находятся из таблицы 2 приложений.
Требуется:
а) Определить оптимальный рацион кормления из условия минимальной стоимости;
б) Учесть дополнительные ограничения, что в рационе содержится: сена - не более 12 кг, силоса - не более 20 кг и концентратов - не более 16 кг.
