2018-01-08
1385
Оценка качества построенного уравнения множественной регрессии, как и в случае парной регрессии, начинается с проверки значимости коэффициентов уравнения. Аналогично случаю парной регрессии, для этой цели используется t-критерий Стьюдента. Для оценки каждого коэффициента регрессии определяются расчетные значения t -статистик Стьюдента:
,
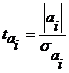где 
- стандартные ошибки коэффициентов уравнения регрессии определяемые по формуле:
.
Расчетные значения t -статистик сравниваются с критическим (табличное) значением tкрит, для определения которого необходимо задать уровень значимости 
(например, 0,05) и число степеней свободы 
= N – n -1 (число наблюдений минус число коэффициентов уравнения).
Если 
, то коэффициент аi является статистически значимым (существенным). В противном случае коэффициент считается незначимым.
Оценка качества построенного уравнения регрессии в целом проводится с помощью F-критерия Фишера. Для этого рассчитывается фактическое (расчетное) значение F - критерия, которое затем сравнивается с критическим значением этого критерия:
.
Для определения критического значения F ‑критерия Фишера 
необходимо задать уровень значимости (например, 0,05), а также два числа степеней свободы 
(количество независимых переменных уравнения) и 
(число наблюдений минус число коэффициентов уравнения).
Если 
, то выявленная зависимость имеет неслучайную природу, а коэффициенты уравнения и показатель тесноты связи статистически значимы. В противном случае выявленная зависимость факторов случайна.
Критерий Фишера позволяет оценить не только качество уравнения множественной регрессии в целом, но и значимость факторов, включаемых в модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, существенно влияет на изменения результирующей переменной у. При наличии в модели нескольких факторов они могут вводиться в модель последовательно, а поскольку между факторами может существовать корреляция, значимость одного и того же фактора может быть разной в зависимости от того, в какой последовательности (т.е. после каких факторов) он попал в модель.
Частный F –критерий Фишера позволяет оценить статистическую значимость присутствия каждого из факторов 
в уравнении множественной регрессии.
Фактические значения частного критерия Фишера для каждого из факторов уравнения множественной регрессии рассчитывают по формуле:
; 
.
Найденные значения 
сравниваются с критическим значением критерия Фишера, найденным в таблице при определении качества построенного уравнения в целом.
Если , то дополнительное включение фактора в уравнение регрессии статистически оправдано. В противном случае включение изучаемого фактора в модель нецелесообразно.
С помощью частного критерия Фишера можно проверить статистическую значимость каждого коэффициента 
уравнения регрессии. В этом случае делается предположение, что соответствующий этому коэффициенту фактор был введен в уравнение последним.
Зная величину , можно определить расчетные значения t -статистик Стьюдента для каждого коэффициента модели множественной регрессии:
и сравнить эти значения с критическим (табличным) tкрит значением.
Для проведения содержательного анализа построенного уравнения регрессии определяют средние коэффициенты эластичности для каждого из факторов:
.
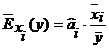Средний коэффициент эластичности результирующей переменной у по переменной показывает, на сколько % в среднем изменится значение зависимой переменной у при изменении значения фактора на 1 % при средних значениях всех остальных независимых факторов.
