Уравнения вида
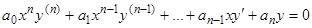 , (9)
, (9)
где все 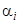 — постоянные, называются уравнениями Эйлера. Уравнение Эйлера заменой независимой переменной
— постоянные, называются уравнениями Эйлера. Уравнение Эйлера заменой независимой переменной 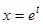 (или
(или 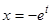 , если
, если 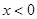 ; в дальнейшем будем считать
; в дальнейшем будем считать 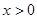 ) преобразуется в линейное однородное уравнение с постоянными коэффициентами.
) преобразуется в линейное однородное уравнение с постоянными коэффициентами.
Действительно, как мы знаем, линейность и однородность уравнения при преобразовании независимой переменной сохраняются, а коэффициенты становятся постоянными, потому что
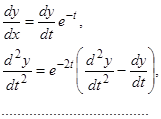
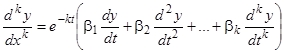 , (10)
, (10)
где все 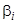 — постоянные, и при подстановке в уравнение (9) множители
— постоянные, и при подстановке в уравнение (9) множители 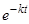 сокращаются с множителями
сокращаются с множителями 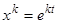 .
.
Справедливость равенства (10) легко может быть доказана методом индукции. Следовательно, линейно входящие в уравнение Эйлера
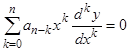 (9.1)
(9.1)
с постоянными коэффициентами произведения 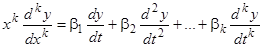 линейно (с постоянными коэффициентами) выражаются через производные функции
линейно (с постоянными коэффициентами) выражаются через производные функции 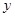 по новой независимой переменной
по новой независимой переменной  . Отсюда следует, что преобразованное уравнение будет линейным однородным уравнением с постоянными коэффициентами
. Отсюда следует, что преобразованное уравнение будет линейным однородным уравнением с постоянными коэффициентами
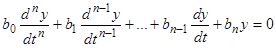 . (11)
. (11)
Вместо того, чтобы преобразовывать уравнение Эйлера в линейное уравнение с постоянными коэффициентами, частные решения которого имеют вид 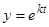 , можно сразу искать решения исходного уравнения в виде
, можно сразу искать решения исходного уравнения в виде 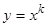 , так как
, так как 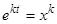 . Получающееся при этом после сокращения на
. Получающееся при этом после сокращения на  уравнение
уравнение
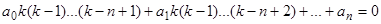 (12)
(12)
для определения  должно совпадать с характеристическим уравнением для преобразованного уравнения (11). Следовательно, корням
должно совпадать с характеристическим уравнением для преобразованного уравнения (11). Следовательно, корням 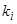 уравнения (12) кратности
уравнения (12) кратности 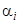 соответствуют решения
соответствуют решения 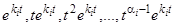 преобразованного уравнения или
преобразованного уравнения или 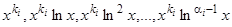 исходного уравнения, а комплексным сопряженным корням
исходного уравнения, а комплексным сопряженным корням 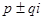 уравнения (12) кратности
уравнения (12) кратности  соответствуют решения
соответствуют решения 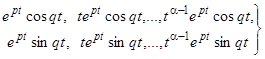 преобразованного уравнения или
преобразованного уравнения или 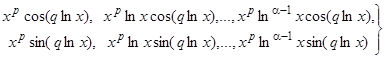 исходного уравнения Эйлера.
исходного уравнения Эйлера.
Пример 7. 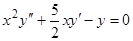 . Ищем решение в виде
. Ищем решение в виде 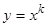 ;
; 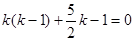 , откуда
, откуда 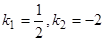 . Следовательно, общее решение при
. Следовательно, общее решение при 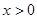 имеет вид
имеет вид 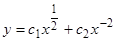 .
.
Пример 8. 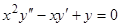 . Ищем решение в виде
. Ищем решение в виде 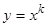 ;
; 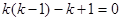 , или
, или 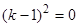 ,
, 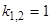 . Следовательно, общее решение при
. Следовательно, общее решение при 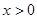 будет
будет 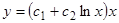 .
.
Пример 9.  . Ищем решение в виде
. Ищем решение в виде 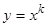 ;
; 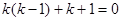 , откуда
, откуда 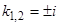 . Следовательно, общее решение при
. Следовательно, общее решение при 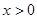 имеет вид
имеет вид  .
.
Уравнения вида 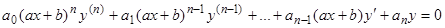 также называются уравнениями Эйлера и сводятся к уравнению (9) заменой независимой переменной
также называются уравнениями Эйлера и сводятся к уравнению (9) заменой независимой переменной 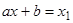 . Следовательно, частные решения этого уравнения можно искать в виде
. Следовательно, частные решения этого уравнения можно искать в виде 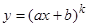 или преобразовать исходное уравнение к линейному однородному уравнению с постоянными коэффициентами заменой переменных
или преобразовать исходное уравнение к линейному однородному уравнению с постоянными коэффициентами заменой переменных 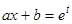 (или
(или 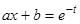 , если
, если 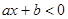 ).
).
 2014-02-02
2014-02-02 1863
1863
