2018-01-08
552
Определение 3.7. Числовая последовательность 
называется бесконечно малой, если 
.
Пример 3.2. Примеры бесконечно малыхчисловых последовательностей:
а) 
; б) 
.
Определение 3.8. Числовая последовательность 
называется бесконечно большой, если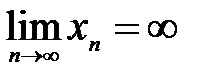 
, то есть, другими словами, если для любого положительного числа 
найдется такое натуральное число 
, что для всех 
выполняется неравенство 
.
Пример 3.3. Примеры бесконечно большихчисловых последовательностей:
а) 
; б) 
.
Основные свойства предела числовой последовательности.
1. Если числовая последовательность имеет предел, то он единственный.
2. Если числовая последовательность имеет предел, то она ограничена.
3. Если числовая последовательность является монотонной и ограниченной, то она имеет предел.
4. Постоянная числовая последовательность, члены которой равны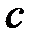 
, сходится к этому числу: 
.
5. Пусть общие члены трехчисловых последовательносте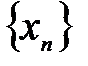й 
, 
и 
удовлетворяют условию 
, 
. Тогда если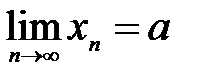 
и 
, то 
.
6. Для того чтобы числовая последовательность 
имела предел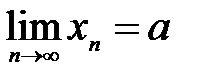 
, необходимо и достаточно, чтобы 
, где 
– бесконечно малая последовательность (
).
