2018-01-08
1633
Определение 3.1. Под числовойпоследовательностью (или просто последовательностью) понимается функция
,
котораязадана на множестве натуральных чисел. Числовая последовательность обозначается в виде 
либо следующим образом: 
, где 
. Число 
– это первый член (элемент) последовательности, число 
– второй член последовательности и т.д., число 
– общий или 
-ый член последовательности.
Числовую последовательность обычно задают формулой ее общего члена, которая позволяет найти любой член по номеру 
. К примеру, выражения
,
задают соответственно числовые последовательности
Определение 3.2. Числовая последовательность 
называется ограниченной, если существует такое число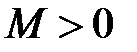 
, что для всех выполняется неравенство
.
Если данное условие не выполняется, то числовая последовательность называется неограниченной. Очевидно, что вышерассмотренные последовательности 
и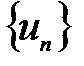 
являются ограниченными, а и 
–неограниченными.
Определение 3.3. Числовая последовательность 
называется возрастающей (неубывающей), если для любого 
выполняется неравенство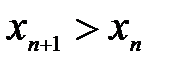 
(
).
|
|
|
Определение 3.4. Числовая последовательность 
называется убывающей (невозрастающей), если для любого 
выполняется неравенство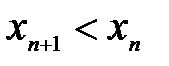 
(
).
Все подобного рода числовые последовательности называются монотонными числовыми последовательностями. Так, последовательности , и 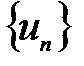являются монотонными, а не является монотонной.
Определение 3.5. Числовая последовательность 
называется постоянной, если все ее элементы равны одному и тому же числу 
.
