2018-01-08
679
«Исследование функций и построение графиков».
Задание 1. Определить интервалы монотонности функций:
1.1.  .
| 1.2.  .
| 1.3.  .
|
1.4.  .
| 1.5.  .
| 1.6.  .
|
Задание 2. Найти точки экстремума функций:
2.1.  .
| 2.2.  .
| 2.3.  .
|
2.4.  .
| 2.5.  .
| 2.6.  .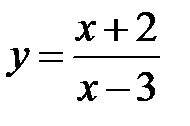
|
Задание 3. Определить наибольшее и наименьшее значение функции на отрезке:
3.1.  ,  .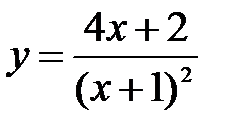
| 3.2.  ,  .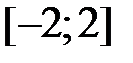
|
3.3.  ,  .
| 3.4.  ,  .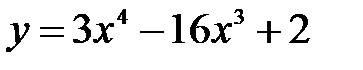
|
3.5.  , .
| 3.6. ,  .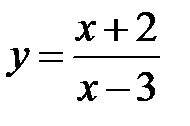
|
Задание 4. Найти точки перегиба и характер выпуклости графика функции:
4.1. 
| 4.2.  .
| 4.3.  .
|
4.4.  .
| 4.5.  .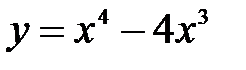
| 4.6. .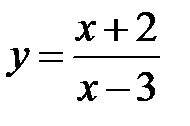
|
Задание 5. Найти уравнение асимптот кривых:
5.1.  .
| 5.2.  .
| 5.3.  .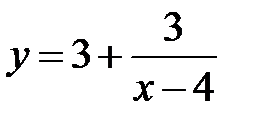
|
5.4.  .
| 5.5.  .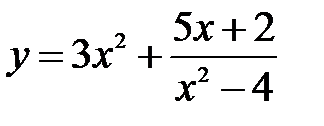
| 5.6. .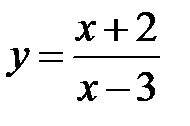
|
Задание 6. Исследовать функции и построить их графики:
6.1.  .
| 6.2.  .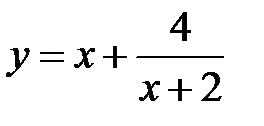
| 6.3.  .
|
6.4.  .
| 6.5.  .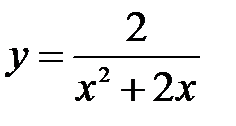
| 6.6.  .
|
6.7.  .
| 6.8.  .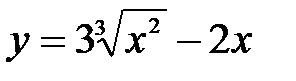
| 6.9.  .
|
6.10.  .
| 6.11. .
| 6.12.  .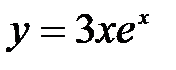
|
6.13.  .
| 6.14.  .
| 6.15.  .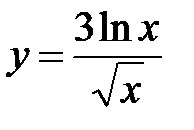
|
6.16.  .
| 6.17.  .
| 6.18.  .
|
Тема 13. ПЕРВООБРАЗНАЯ ФУНКЦИИ.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Понятие первообразной и неопределенного интеграла.
Определение 13.1. Функция 
называется первообразной функции 
на некотором интервале, если для любого 
из этого интервала выполняется равенство
.
Любая непрерывная функция 
имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.
Определение 13.2. Совокупность всех первообразных 
, где 
− произвольная постоянная, называется неопределенным интегралом и обозначается следующим образом: 
.Здесь называется подынтегральной функцией, 
– подынтегральным выражением, 
– переменной интегрирования.
Определение 13.3. Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
