Выпуклость и вогнутость графика функции. Точки перегиба

Определение 12.6. Гладкая кривая вогнутав точке , если существует окрестность этой точки , в которой кривая расположена выше касательной, проведенной в этой точке.

Определение 12.7. Гладкая кривая выпуклав точке , если существует окрестность этой точки , в которой кривая расположена ниже касательной, проведенной в этой точке.

Определение 12.8. Точка графика функции , при переходе через которую график меняет выпуклость на вогнутость и наоборот, называется точкой перегиба.

Теорема 12.2. Кривая вогнута на интервале , если в каждой точке этого интервала выполнено условие

при

и выпукла, если

при

Схема исследования функции на выпуклость и вогнутость и наличие точек перегиба:

1. Найти вторую производную от данной функции .

2. Найти критические точки на перегиб, в которых вторая производная или не существует.

3. Найти знаки второй производной. Определить интервалы выпуклости и вогнутости.

4. Сделать вывод о наличии точек перегиба.

Пример 12.3. Найти точки перегиба функции .

Решение:

1. Найдем первую и вторую производные заданной функции:

,

.

2. Найдем точки, в которых

вторая производная равна нулю– :

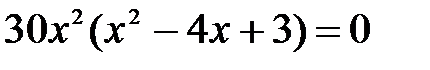при , и ;

вторая производная не существует – таких точек нет.

Значит, критические точки на перегиб: , и .

3. Исследуем изменение знака второй производной:

на интервале ,на интервалах , и .

Таким образом, точки 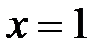и – точки перегиба.