2018-01-08
6498
Изучение заданной функции и построение ее графика целесообразно проводить в следующем порядке:
1. Найти область определения функции.
2. Исследовать функцию на четность – нечетность.
3. Исследовать функцию на периодичность.
4. Найти точки пересечения с осями координат.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости и вогнутости и точки перегиба.
7. Найти асимптоты графика функции.
8. При необходимости найти некоторые дополнительные точки, уточняющие график функции.
9. Построить график на основе проведенного исследования.
Пример 12.2. Исследовать функцию 
и построить ее график.
Решение:
1. Найдем область определения функции.
Данная функция имеет смысл, если знаменатель отличен от нуля:
; 
; 
.
Таким образом, областью определения функции является множество всех действительных чисел, кроме 
, т.е. 
.
2. Исследуем функцию на четность – нечетность.
Поскольку 
, то функция четная, а ее график симметричен относительно оси ординат.
3. Исследуем функцию на периодичность.
Данная функция не является периодической.
4. Найдем точки пересечения с осями координат.
Точка пересечения с осью ординат– 
: 
.
Точка пересечения с осью абсцисс– 
: 
. Это уравнение на области определения решений не имеет, следовательно, график функции не пересекает ось абсцисс.
5. Найдем экстремумы и интервалы монотонности функции.
· Найдем производную заданной функции:
· Найдем точки, в которых
производная равна нулю –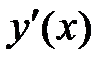 
=0: 
при 
;
производная не существует: 
при 
.
Однако критической является только точка 
, так как значения 
не входят в область определения функции.
· Исследуем изменение знака производной при переходе через критическую точку:
при 
,при 
.
Таким образом, 
– точка минимума, а 
– минимум функции; на интервалах 
и 
функция убывает, на интервалах 
и 
функция возрастает.
6. Найдем интервалы выпуклости и вогнутости и точки перегиба.
· Найдем вторую производную заданной функции:
.
· Найдем точки, в которых
вторая производная равна нулю – 
=0: 
– это уравнение на области определения решений не имеет;
вторая производная не существует: 
при 
.
Критических точек на перегиб нет, так как значения 
не входят в область определения функции.
· Исследуем изменение знака второй производной:
на интервалах 
и 
,на интервале 
.
Таким образом, точек перегиба нет; на интервалах и график функции выпуклый, а на интервале – вогнутый.
7. Найдем асимптоты.
· Исследуем поведение функции вблизи точек разрыва 
:
, следовательно, прямая 
есть вертикальная асимптота. В силу симметричности графика функции 
также вертикальная асимптота.
· Выясним поведение функции на бесконечности:
.
Таким образом, прямая 
– горизонтальная асимптота.
· Найдем наклонную асимптоту.
.
Таким образом, наклонных асимптот нет.
9. График функции изображен на рисунке 12.1.
Рис. 12.1.График функции .
