Дискриминант квадратного уравнения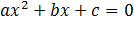

Дискриминант квадратного уравнения - выражение 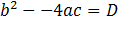- по знаку которого судят о наличии этого уравнения действительных корней. Различные возможные случаи в зависимости от значения D.

1. Если D>0, то уравнение имеет два корня: 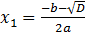и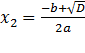

Пример: Рассмотрим уравнение 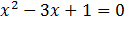, где а=2; b= -3; с=1

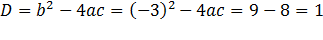; 2 корня

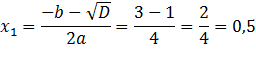
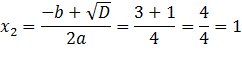
Ответ: 0,5 и 1

2. Если D= 0, то уравнение имеет один корень: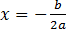

Пример: Рассмотрим уравнение 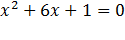, где а=9; b= 6; с=1

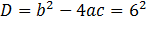
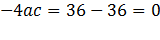; 1 корень

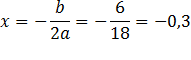
Ответ: - 0,3

3. Если D <0, то уравнение не имеет корней.

Пример: Рассмотрим уравнение 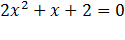, где а=2; b=1; с=2,

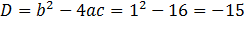, корней нет.

Теорема Виета

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета.Используя теорему Виета, можно выразить сумму и произведение корней произвольного квадратного уравнения через его коэффициенты.

Приведенное квадратное уравнение 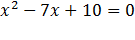имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. На примере видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Необходимо доказать, что любое приведенное квадратное уравнение, имеющее корни, обладает таким свойством.

Если уравнение не приведенное, например 2 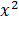+3x+8=0 его можно сделать приведенным. Для этого мы все уравнение поделим на первый коэффициент и получим: 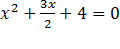и решаем как обычно.

Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Приведенное квадратное уравнение имеет вид: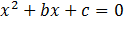

Обозначим второй коэффициент буквой р, а свободный член буквой q: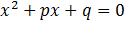

Дискриминант этого уравнения D равен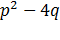

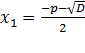и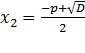

Найдем сумму и произведение корней

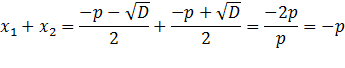
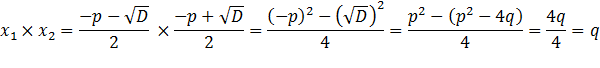
Следовательно,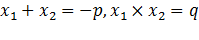

Пример:рассмотрим уравнение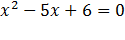

D =1, уравнение имеет два корня, 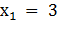и 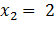, p= -3; q= 2.

По теореме Виета 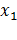+ 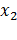= - p, значит ;

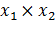= q, значит .

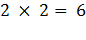Следовательно,x₁ = 2 и x₂ = 1 являются корнями уравнения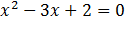

При D = 0 корни уравнения можно вычислить по формуле.

Квадратное уравнение 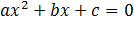имеет корни х₁ и х₂ равносильное ему приведенное квадратное уравнение имеет вид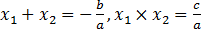

Справедливо утверждение, обратное теореме Виета:

Теорема: Если числа m и n таковы, что их сумма равна -p, а произведение равно q, то эти числа являются корнями уравнения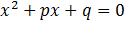

По условию, m+n=-p, a m 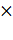n=q. Значит, уравнение 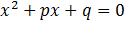можно записать в виде 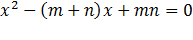. Подставив вместо х число, получим: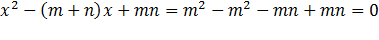

Значит, число m является корнем уравнения. Аналогично можно показать, что число n также является корнем уравнения.

Пример: рассмотрим уравнение

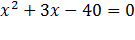
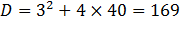
По формуле корней квадратного уравнения получаем:

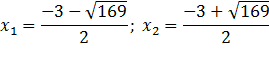
отсюда х₁= -8; х₂= 5.

Покажем, что корни уравнения найдены правильно. В уравнении 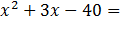0 коэффициент р равен 3, а свободный член q равен -40. Сумма найденных чисел - 8 и 5 равна -3, а их произведение равно -40. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения уравнении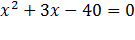

7) Способы рационального решения квадратного уравнения

Свойства коэффициентов квадратного уравнения.

1) Еслиа+ b+c= 0, то 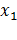=1,

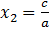
Пример: рассмотрим уравнение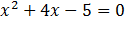

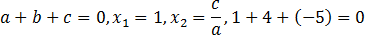
Значит корнями этого уравнения являются 1 и -5. Проверим это с помощью нахождения дискриминанта

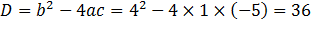
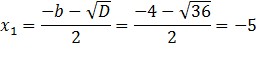
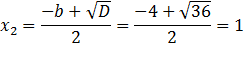
Отсюда следует, что еслиа+b+c= 0,то ,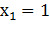

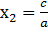
2) Еслиb= а+c, то 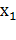= –1, =

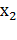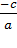
Пример: рассмотрим уравнение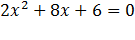

Если b= а+c, то ,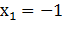

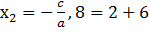
Значит корнями этого уравнения являются -1 и -3. Проверим это с помощью нахождения дискриминанта: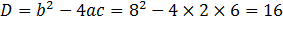

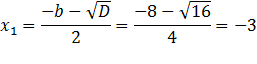
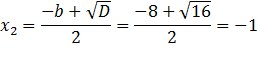
Отсюда следует, что если b= а+c, то ,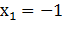

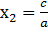
Способ переброски

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а±b+c≠0, то используется прием переброски:

 

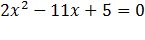
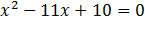
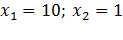,корни уравнения необходимо поделить на 2.

Ответ: 5; 0,5.