Графическое решение квадратного уравнения

Если в уравнении 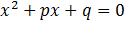перенести второй и третий члены в правую часть, то получим

Построим графики зависимостей и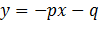

График первой зависимости - парабола,проходящая через начало координат. График второй зависимости - прямая.Возможны следующие случаи:прямая и парабола могут пересекаться в двух точках, абсциссыточек пересечения являются корнями квадратного уравнения;

- прямая и парабола могут касаться (только одна общая точка),т.е.уравнение имеет одно решение;

- прямая и парабола не имеют общих точек, т.е. квадратноеуравнение не имеет корней.

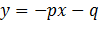
х₁ х₂ х

Пример: решим графически уравнение

Запишем уравнениев виде

Построим параболу и прямую .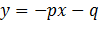

Прямую можно построить по двум точкам М (0;4) и N (3;13).

Прямая и парабола пересекаются в двух точках А и B с абсциссам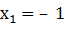и и .

11)Решение квадратных уравнений с помощью циркуля и линейки

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика. Предлагаю следующий способ нахождения корней квадратного уравнения с помощью циркуля и линейки.

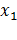Допустим, что искомая окружность пересекает осьабсцисс в точках B и D , где и 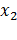- корни уравнения , и проходит через точки А(0; 1) и C на оси ординат. Тогда по теореме о секущих имеемOB OD=AO OC, откуда OC=OB OD/OA=x₁ x₂/1= .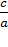

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

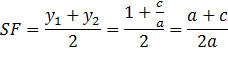
Итак:

1) построим точки (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.

2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох в точке В(; 0), где - корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.

a)AS>SB,R> .

Два решения x₁и x₂

б) AS=SB,R= .

Одно решение x₁.

в) AS<SB,R< .

Нет решений.

Пример:

Решим уравнение

Определим координаты точки центра окружности по формулам:

x=

y=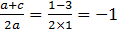

Проведем окружность радиуса SA, где А (0; 1).

Ответ: х₁ = - 1; х₂ = 3.