Способы решения квадратных уравнений

1)Решение квадратных уравнении при b=0

Неполные квадратные уравнения, у которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).

Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.

(

Приравнием к нулю каждый из множителей:

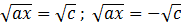
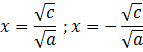
Пример:

1)

Раскладываем левую часть уравнения по формуле разности квадратов:

Это уравнение — типа «произведение равно нулю» приравниваем к нулю каждый множитель:

;

;

;

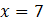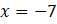
Ответ: 7; -7.

2)Решение квадратных уравнении при с=0

Такие уравнения решаются разложением левой части уравнения на множители.

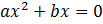
Общий множитель xвыносим за скобки:

Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

;

Второе уравнение — линейное. Решаем его:

/

 

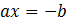; Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — .

Пример:

1)

Общий множитель x выносим за скобки:

Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

Ответ: 0; -18.