Отношение делимости на множестве целых неотрицательных чисел, его свойства

Пусть даны натуральные числа a и b. Говорят, что число a делится на число b, если существует такое натуральное число q, что a = bq.

В этом случае число b называют делителем числа а, а число а – кратным числа b. Например, 24 делится на 8, так как существует такое q = 3, что 24 = 8*3. Можно сказать иначе: 8 – это делитель числа 24, а 24 есть кратное числа 8. В случае, когда а делится на b, пишут: 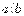. Эту запись часто читают и так: «а кратно b». Свойства делимости Известно, что отношение делимости на множестве N обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства. Теорема. Отношение делимости антисимметрично, т.е. 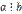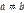если и , то 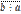. Доказательство. Предположим противное, т. е. что 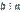. Но тог­да 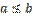, согласно теореме, рассмотренной выше.

По условию 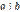и 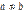. Тогда, по той же теореме, 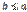. Неравенства 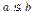и 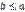будут справедливы лишь тогда, когда 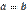, что противоречит условию теоремы. Следовательно, наше предпо­ложение неверное и теорема доказана. Теорема. Отношение делимости транзитивно, т.е. если и , то 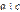. Доказательство. Так как 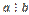, то существует такое натуральное число q, что а = bq, а так как 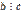, то существует такое натуральное число p, что 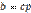. Но тогда имеем: 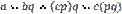. Число pq – натуральное. Значит, по определению отношения делимости, 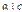. Теорема (признак делимости суммы). Если каждое из натураль­ных чисел а1, а2..., ап делится на натуральное число b, то и их сумма а1 + а2 +... + ап делится на это число. Доказательство. Так как 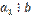, то существует такое натураль­ное числ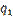о что 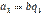. Так как 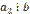, то существует такое нату­ральное числ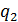о ,что 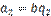. 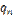Продолжая рассуждения, получим, что если , то существует такое натуральное число , что 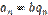. Эти равенства позволяют преобразовать сумму а1 + а2 +... + ап в сумму вида bq1 + bq2 +... + bqn. Вынесем за скобки общий множитель b, а получившееся в скобках натуральное число q1 + q2 +... + qn обозначим буквой q. Тогда а1 + а2 +... + ап = b(q1 + q2 +... + qn) = bq, т.е. сумма а1 + а2 +... + ап оказалась представленной в виде произведения числа b и некоторого натурального числа q. А это значит, что сумма а1 + а2 +... + ап делится на b, что и требовалось доказать. Теорема (признак делимости разности). Если числа а1 и а2 делятся на b и 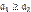, то их разность 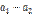делится на b.