2018-01-08
1383
а) Пусть на плоскости 
дана фигура, ограниченная отрезком [a;b] оси 
, прямыми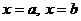 
и графиком непрерывной и неотрицательной функции 
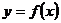на [a;b] (рис. 1).
Рисунок 1
Это криволинейная трапеция, площадь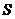 
которой может быть вычислена по формуле 
(1).
б) Пусть фигура ограничена снизу и сверху графиками функций 
и 
, 
, 
(рис.2), где 
и 
- две непрерывные функции (рис. 2).
|
|
Рисунок 2
Тогда 
(2)
Пример 1
Найти площадь фигуры, ограниченной линиями 
, 
, 
, 
.
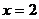Решение. Данная фигура является криволинейной трапецией (рис.3).
Рисунок 3
Поэтому ее площадь вычисляется по формуле (1).
.
Ответ. 
.
Пример 2
Вычислить площадь фигуры, ограниченной линиями: 
.
Решение. Данная фигура заключена между графиками функций 
, осью при условии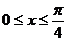 
(рис.4).
Рисунок 4
Ее площадь 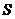складывается из площадей 
и 
криволинейных трапеций. Найдем абсциссу точки А из условия 
или 
. Учитывая, что 
имеем и 
.
Ответ. 
Пример 3
Найти площадь фигуры, ограниченной линиями 
Решение. Данная фигура заключена между графиками функций 
прямыми 
и 
(рис.5).
Рисунок 5
Поэтому ее площадь находим с помощью формулы (2).
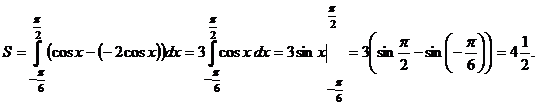
Ответ. 
Длина дуги кривой
Если функция 
непрерывна вместе с 
на отрезке [a;b], то длина L дуги АВ выражается формулой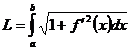 
.
При параметрическом задании кривой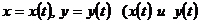 
-непрерывно дифференцируемые функции) длина дуги кривой, соответствующая изменению параметра 
от 
до 
вычисляется по формуле 
.
Если гладкая кривая задана в полярных координатах уравнением 
то длина дуги равна 
.
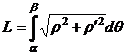Пример 1
Вычислить длину дуги кривой 
от 
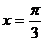до 
Решение. Применяя формулу длины дуги кривой, имеем 
, где 
.
Тогда 
, так как 
- угол I четверти и 
Таким образом
Ответ: 
.
Пример 2
Вычислить длину дуги кривой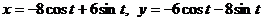 
от 
до 
.
Решение. Так как кривая задана параметрическими уравнениями, то 
.
Упростим подынтегральное выражение 
Тогда 
Ответ: 
Пример 3
Вычислить длину дуги кривой 
.
Решение.
Так как кривая задана уравнением в полярных координатах, то длина дуги равна 
.
Поскольку уравнение задает окружность (рис.6), то пределы интегрирования 
и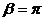 
.
|
Рисунок 6
Ответ: 
.
Пусть функция непрерывна и неотрицательна на отрезке [a;b]. Тогда тело, которое образуется вращением вокруг оси криволинейной трапеции, ограниченной сверху графиком функции 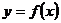, имеет объем 
.
Если фигура, ограниченная кривыми 
и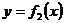 
и прямыми 
вращается вокруг оси 
то объем тела вращения 
Объем тела, полученного вращением криволинейной трапеции 
вокруг оси 
вычисляется по формуле 
Пример 1
Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями 
Решение.
Уравнение 
определяет параболу, вершина которой находится в точке 0(0;0). Применяя формулу объема тела вращения, имеем 
Ответ. 
Пример 2
Найти объем тела, образованного вращением вокруг оси фигур, ограниченных линиями: 
Решение.
Построим линии, ограничивающие фигуры и заметим, что объем тела, образованного вращением вокруг оси этих фигур находится как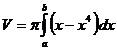 
(рис. 7).
Рисунок 7
Пределы интегрирования 
и 
определяются как абсциссы точек пересечения линий 
и 
т.е. 
Тогда 
Ответ.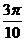 
.
Пример 3
Найти объем тела, образованного вращением вокруг оси 
фигуры, ограниченной линиями 
Решение.
Так как тело получено вращением фигуры вокруг оси то применяем формулу 
(рис.8).
|
|
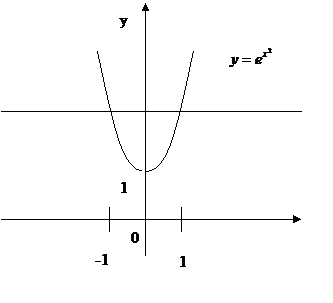
Рисунок 8
Определим нижний предел интегрирования: при 
Таким образом 
по условию.
Функцию 
запишем в виде 
.
Рассмотрим часть линии, расположенную в I четверти, где 
Тогда 
Вычислим полученный интеграл методом интегрирования по частям.
Пусть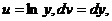 
тогда 
и 
Ответ. 
