Определение и свойства определенного интеграла

ОГЛАВЛЕНИЕ

Введение

1 Понятие определенного интеграла………………………………………4

1.1 Определение и свойства определенного интеграла ………………..4

1.2 Вопросы для самопроверки ……………. …………………………..6

1.3Примеры для самостоятельного решения………………………….. 6

2 Замена переменной и формула интегрирования по частям в определенном интеграле…………………………………………………………………..6

2.1 Замена переменной в определенном интеграле……………………..6

2.2 Формула интегрирования по частям в определенном интеграле…..8

2.3 Вопросы для самопроверки…………………………………………..10

2.4 Примеры для самостоятельного решения…………………………...11

3 Некоторые геометрические и физические приложения определенного интеграла………………………………………………………………......12

3.1 Площадь криволинейной трапеции………………………………….12

3.2 Длина дуги кривой……………………………………………………16

3.3 Объем тела вращения………………………………………………....18

3.4 Площадь поверхности вращения…………………………………….20

3.5 Работа переменной силы……………………………………………..22

3.6 Вопросы для самопроверки…………………………………………..23

3.7 Примеры для самостоятельного решения…………………………...24

4 Несобственные интегралы……………………………………………….24

4.1 Несобственные интегралы с бесконечными пределами

интегрирования……………………………………………………….24

4.2 Несобственные интегралы от неограниченных функций………….26

4.3 Вопросы для самопроверки……………………………………….....27

4.4 Примеры для самостоятельного решения…………………………..27

ВВЕДЕНИЕ

Цель настоящих методических указаний - изложение основных приемов вычисления определенных интегралов и иллюстрация их на примерах с подробными пояснениями.

Важность темы «Определенный интеграл» для студентов аграрного университета очевидна благодаря огромному числу приложений таких интегралов в различных разделах физики, механики, гидравлики и других наук.

Методические указания содержат: краткие теоретические сведения, решение типовых примеров, вопросы для самопроверки и список рекомендуемой литературы.

Понятие определенного интеграла

Определение и свойства определенного интеграла

Пусть 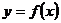- функция, определенная на отрезке [a;b]. Разобьём этот отрезок на n произвольных частей точками . Обозначим , где , .

В каждом из полученных отрезков выберем произвольную точку ξ и составим интегральную сумму .

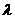Если предел при стремлении к нулю существует и не зависит от способа разбиения отрезка точками на части и от выбора точек , то он называется определенным интегралом от функции в пределах от до и обозначается .

Таким образом, .

На практике определенный интеграл вычисляется по формуле Ньютона-Лейбница (1), где первообразная функции . Формула (1) применяется, когда известна первообразная и ее вычисление при и 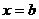не вызывает затруднений. Применяются обозначения .

Основные свойства определенного интеграла

1. ,

2.

3. Каковы бы ни были числа a, b, c имеет место равенство

4.

5.

Пример 1

Вычислить .

Решение. Первообразные функций и известны: ; поэтому, используя свойство 5, получаем .

Ответ.

Пример 2

Вычислить .

Решение. По правилам интегрирования тригонометрических выражений имеем

Ответ.

Вопросы для самопроверки

1. Что понимается под интегральной суммой?

2. Что называется определенным интегралом от функции ?

3. Как на практике вычисляется определенный интеграл?

4. Перечислите основные свойства определенного интеграла.