2018-01-08
965
1. Найти площадь фигуры, ограниченной равнобочной гиперболой 
, осью 
и прямыми 
, 
.
2. Найти площадь области, ограниченной одной аркой циклоиды 
, 
и осью абсцисс.
3. Вычислить площадь области, ограниченной одной пятой кривой 
4. Найти объем тела, образованного вращением окружности 
вокруг оси 
.
5. Фигура, ограниченная одной аркой циклоиды 
и осью , вращается вокруг оси . Найти объем тела вращения.
6. Та же фигура, что и в задаче 5, вращается вокруг оси 
. Найти объем тела вращения.
7. Найти длину дуги кривой 
пределах от 
до 
.
8. Найти длину координаты 
.
9. Найти площадь поверхности конуса, образуемого вращением отрезка прямой 
от до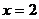 
а) вокруг оси , б) вокруг оси .
10. Найти площадь поверхности тела, образованного вращением кардиоиды вокруг оси . Кардиоида задана параметрическими уравнениями 
11.Вычислить работу, которую нужно затратить, чтобы выкачать жидкость плотностью 
из резервуара, имеющего форму обращенного вершиной к низу конуса, высота которого H, а радиус основания R.
12.Вычислить работу, необходимую для того, чтобы выкачать воду из полусферического сосуда, диаметр которого равен 20 м.
|
|
|
Несобственные интегралы
