2018-01-08
227
Определение. Системой линейных уравнений, состоящей из m уравнений с n неизвестными 
, называется система вида
где 
– некоторые числа.
Определение. Матрицей системы называется матрица
.
Определение. Столбцом свободных членов называется вектор-столбец
.
Определение. Столбцом неизвестных называется вектор-столбец
.
Тогда в матричной записи система линейных уравнений может быть записана в виде 
.
Определение. Расширенной матрицей системы называется матрица, полученная приписыванием к А справа после вертикальной черты столбца свободных членов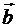 
, обозначаемая (А | ).
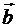Определение. Система линейных уравнений называется однородной, если свободные члены всех ее уравнений равны нулю, и неоднородной – в противном случае.
Определение. Решением системы линейных уравнений называется упорядоченный набор n чисел (n -мерный вектор-столбец) 
, при подстановке которого в систему линейных уравнений вместо 
получаем систему тождеств.
Определение. Общим решением системы линейных уравнений называется совокупность всех ее решений.
Определение. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае.
Специальный случай.
Рассмотрим системы линейных уравнений с квадратной матрицей, определитель которой неравен нулю.
Теорема (правило Крамера). Система из n уравнений с n неизвестными в случае, когда определитель матрицы системы отличен от нуля, имеет решение, и притом только одно. Это решение находится по формулам
(для всех 
),
где через 
обозначен определитель матрицы системы, а через 
– определитель матрицы, полученной из матрицы системы заменой i - го столбца столбцом свободных членов.
Доказательство. Возьмем расширенную матрицу системы и припишем к ней сверху произвольную ее строку, например j -ю. В результате получится квадратная матрица порядка n +1. В этой матрице две одинаковые строки, и поэтому ее определитель равен нулю:
=0.
