Определение. Суммой двух матриц А и В одинаковой размерности m × n называется матрица С той же размерности, элементы которой равны  (
( ;
;  ).
).
Для обозначения суммы двух матриц используется запись  . Операция получения суммы матриц называется их сложением.
. Операция получения суммы матриц называется их сложением.
Теорема. Сложение матриц коммутативно, т. е. 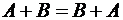 .
.
Доказательство. Пользуясь определением суммы двух матриц и коммутативностью сложения чисел  , убеждаемся в очевидности данного утверждения.■
, убеждаемся в очевидности данного утверждения.■
Теорема. Сложение матриц ассоциативно, т. е.
 .
.
Доказательство. Пользуясь определением суммы двух матриц и ассоциативностью сложения чисел, убеждаемся в очевидности данного утверждения.■
Эти теоремы позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.
Определение. Произведением матрицы А (размерности m × n) на действительное число 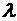 называется матрица С той же размерности, элементы которой равны
называется матрица С той же размерности, элементы которой равны  (
( ;
;  ).
).
Для обозначения произведения матрицы на число используется запись  или
или  . Операция получения произведения матрицы на число называется умножением матрицы на это число.
. Операция получения произведения матрицы на число называется умножением матрицы на это число.
Теорема. Умножение матрицы на число ассоциативно относительно числового множителя, т. е.  .
.
Доказательство. Пользуясь определением произведения матрицы на число и ассоциативностью умножения чисел, убеждаемся в очевидности данного утверждения.■
Теорема. Умножение матрицы на число дистрибутивно относительно сложения матриц, т. е.  .
.
Доказательство. Пользуясь определением произведения матрицы на число и дистрибутивностью умножения чиселотносительно их сложения, убеждаемся в очевидности данного утверждения.■
Теорема. Умножение матрицы на число дистрибутивно относительно сложения чисел, т. е.  .
.
Доказательство. Пользуясь определением произведения матрицы на число и дистрибутивностью умножения чиселотносительно их сложения, убеждаемся в очевидности данного утверждения.■
Определение. Разностью двух матриц А и В одинаковой размерности m×n называется матрица С той же размерности, которая в сумме с матрицей В дает матрицу А.
Для обозначения разности двух матриц используется запись  . Операция получения разности матриц называется их вычитанием. Легко убедиться, что разность С двух матриц А и В может быть получена по правилу
. Операция получения разности матриц называется их вычитанием. Легко убедиться, что разность С двух матриц А и В может быть получена по правилу  .
.
Определение. Нулевой (не по внешнему виду, а по роли в алгебраической структуре) называется такая матрица О, что для любой матрицы А верно  .
.
Легко убедиться, что единственной такой матрицей является матрица, которую мы раньше назвали нулевой по внешнему виду, т. е. матрица размерности той же, что и А, состоящая из одних нулей.
Определение. Противоположной к матрице А называется такая матрица (– А) той же размерности, что и А, для которой верно  .
.
Легко убедиться, что (– А)=  – единственная такая матрица для каждой матрицы А. Если А = О, то она противоположна сама себе.
– единственная такая матрица для каждой матрицы А. Если А = О, то она противоположна сама себе.
Определение. Произведением матрицы А, имеющей размерность m × n, на матрицу В, имеющую размерность n × p, называется матрица С, имеющая размерность m × p, элементы которой равны  (
( ;
;  ;
;  ).
).
Для обозначения произведения матрицы А на матрицу В используют запись  . Операция получения произведения матрицы А на матрицу В называется перемножением этих матриц.
. Операция получения произведения матрицы А на матрицу В называется перемножением этих матриц.
Матрицу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В. Оба произведения  и
и  можно определить лишь в том случае, когда число столбцов А совпадает с числом строк В, число строк А совпадает с числом столбцов В. При этом обе матрицы
можно определить лишь в том случае, когда число столбцов А совпадает с числом строк В, число строк А совпадает с числом столбцов В. При этом обе матрицы  и
и  будут квадратными, но размерности их будут, вообще говоря различными. Для того чтобы оба произведения
будут квадратными, но размерности их будут, вообще говоря различными. Для того чтобы оба произведения  и
и  не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы А и В были квадратными матрицами одного и того же порядка.
не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы А и В были квадратными матрицами одного и того же порядка.
Теорема. Умножение матриц (при условии, что оно определено) ассоциативно, т. е.
 .
.
Доказательство. Чтобы произведения были возможны, необходимо, чтобы матрица А имела размерность m × n, матрица В имела размерность n × p, а матрица С имела размерность p × r. Тогда элемент  матрицы
матрицы  равен
равен  , а элемент
, а элемент 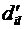 матрицы
матрицы  равен
равен  . Равенство
. Равенство  вытекает из возможности изменения порядка суммирования относительно j и k. ■
вытекает из возможности изменения порядка суммирования относительно j и k. ■
Теорема. Умножение матриц (при условии, что оно определено) дистрибутивно относительно сложения матриц, т. е.  или
или  .
.
Доказательство. Пользуясь определениями перемножения и сложения матриц и дистрибутивностью умножения чиселотносительно их сложения, убеждаемся в очевидности данного утверждения.■
Вопрос о коммутативности произведения матрицы А на матрицу В имеет смысл ставить лишь для квадратных матриц А и В одинаковой размерности, поскольку только для таких матриц А и В оба произведения АВ и ВА определены и являются матрицами одинаковых порядков.
Легко убедиться, что произведение двух квадратных матриц, вообще говоря, некоммутативно.
Действительно, пусть  ,
,  . Тогда АВ =
. Тогда АВ =  ВА =
ВА =  .
.
Определение. Единичной (не по внешнему виду, а по роли в алгебраической структуре) называется такая матрица Е, что для любой квадратной матрицы А верно  или
или  .
.
Легко убедиться, что единственной такой матрицей является матрица, которую мы раньше назвали единичной по внешнему виду, т. е. матрица размерности той же, что и А, у которой элементы главной диагонали равны единице, а все остальные – нулю. Действительно, если предположить, что  – другая единичная матрица, то по определению
– другая единичная матрица, то по определению  . Причем
. Причем  , т. е. матрица Е является как левой единичная, так и правой единичной матрицей, поскольку коммутирует с любой квадратной матрицей.
, т. е. матрица Е является как левой единичная, так и правой единичной матрицей, поскольку коммутирует с любой квадратной матрицей.
Обратная матрица
Определение. Обратной к квадратной матрице А называется такая матрица  той же размерности, что и А, для которой верно
той же размерности, что и А, для которой верно  или
или  .
.
Легко убедиться, что если для матрицы А существует правая обратная матрица В, т. е.  , то она единственная, и существует левая обратная матрица С, которая совпадает с В, т. е.
, то она единственная, и существует левая обратная матрица С, которая совпадает с В, т. е.  . Действительно, равенства
. Действительно, равенства  показывают, что всякая левая обратная матрица С совпадает с В. Аналогично показывается, что всякая правая обратная матрица совпадает с С, а на основании выше доказанного, совпадает и с В.
показывают, что всякая левая обратная матрица С совпадает с В. Аналогично показывается, что всякая правая обратная матрица совпадает с С, а на основании выше доказанного, совпадает и с В.
Остался открытым вопрос существования обратной матрицы.
Определение. Невырожденной называется матрица, определитель которой отличен от нуля.
Теорема. Обратная матрица существует у невырожденных матриц и только у них.
Доказательство. Пусть матрица А – невырожденная, т. е.  . Тогда существует матрица
. Тогда существует матрица
 ,
,
где  – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 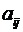 , определяемое как
, определяемое как  =
= 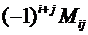 , где
, где 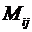 – минор элемента
– минор элемента 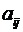 . Покажем, что матрица В является обратной для А, т. е. матрица С = АВ является единичной.
. Покажем, что матрица В является обратной для А, т. е. матрица С = АВ является единичной.

поскольку матрица  имеет две одинаковых строки
имеет две одинаковых строки 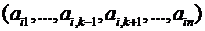 . Таким образом, С = Е. ■
. Таким образом, С = Е. ■
Одним из способов вычисления обратной матрицы является следующий.
1. Составить расширенную матрицу (А | Е), приписав после матрицы А за вертикальной чертой единичную матрицу той же размерности, что и А.
2. Матрицу (А | Е) с помощью элементарных преобразований строк привести к ступенчатому виду Гаусса.
Если при этом на месте матрицы А получилась матрица Е, то за вертикальной чертой находится матрица  . В противном случае
. В противном случае 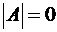 и матрица
и матрица  не существует.
не существует.
 2018-01-08
2018-01-08 1577
1577
