Формальне представлення стійкості динамічних систем

 

Для складних систем, зокрема економічних, стійкість означає, що при виникненні збурювання, що злегка виводить систему зі стану рівноваги, система буде прагнути до відновлення колишнього стану, тобто всі її наступні стани будуть перебувати поблизу стану рівноваги (рис. 4.1).

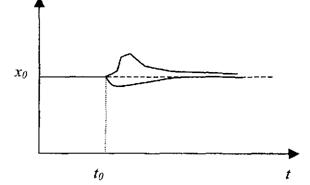
Рис. 4.1. Стійкість для динамічної системи

 

Формалізація питань стійкості реалізується у вигляді кілька визначень.

Розглянемо систему, описувану диференціальним рівнянням (системою диференціальних рівнянь) виду

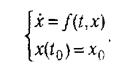(4.1)

Визначення 1. Система (4.1) називається автономною, якщо змінна часу не входить у її праву частину безпосередньо. B противному випадку система називається неавтономною.

Допустимо, що функція f(x, t) має необхідні властивості, щоб система (4.1) мала єдине рішення

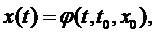(4.2)

Визначення 2. Стан системи х_е називається станом рівноваги системи (4.1), якщо

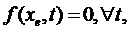(4.3)

або

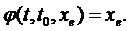(4.4)

Це визначення означає, що система сама по собі (при відсутності зовнішнього впливу) не покине стан рівноваги.

Визначення 3. Стан рівноваги х_е динамічної системи (4.1) називається стійким по Ляпунову (стабільним), якщо

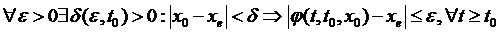(4.5)

Це визначення означає, що завжди можна вибрати таке початкове положення системи х₀, що відрізняється від стану рівноваги менш, ніж на 8, що всі крапки траєкторії системи будуть перебувати від стану рівноваги не далі e(рис. 4.2).

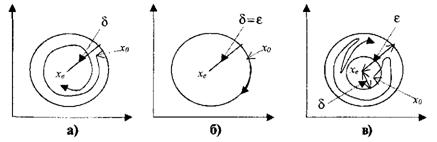
Рис. 4.2. Стійкість по Ляпунову

 

Визначення 4. Крапка рівноваги x_e динамічної системи (4.1) називається асимптотично стійкою, якщо:

1) вона є стійкою в змісті визначення 3;

2) виконано

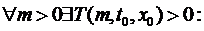
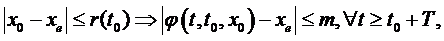
де r (t₀)> 0 – константа

Іншими словами

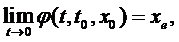(4.6)

Таким чином, до асимптотично стійкої крапки рівноваги сходиться при t®¥ будь-яка траєкторія, що починається істотно близько до неї (рис. 4.3).

Асимптотична стійка крапка називається аттрактором («притягуюча»), а нестабільна — репеллером (рис. 4.4).

Число r(t₀) називається базисом аттрактора.

 

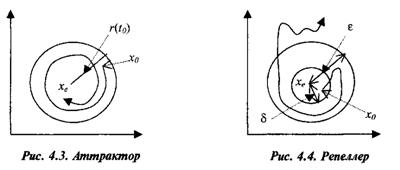
Визначення 5. Стан рівноваги х_е динамічної системи (4.1) називається в цілому асимптотично стійким, якщо

1) воно є стійким;

2) будь-яка траєкторія при t сходиться до х_е, якщо ïx₀ – x_e­ï£r,
де r > 0 — постійне, досить велике число (рис. 4.5).

Якщо константи у визначеннях 3, 4, 5 (d,T, r) не залежать від t₀, то говорять про однорідну стійкість.

Для простоти викладу надалі будемо вважати, що система (4.1) має нульове рішення.

Рис. 4.5. В цілому асимптотично стійкий стан

Теорема Ляпунова про стійкість.

Нехай для системи (4.1) існує така функція V(x), безперервно диференційована в околиці точки x=0, що

1) V(0)=0,

2) V(x)>0, х¹0;

3) в області завдання системи (4.1), тоді рішення х=0 є стійким.

Теорема Ляпунова дозволяє також визначити необхідні умови стійкості параметризованих систем, зокрема, для загальної рівноваги Вальраса.