Стохастична стійкість

 

Детерміністична теорія стійкості являє собою один з розділів якісної теорії динамічних систем. Більшість результатів стосується певних якісних або кількісних (але не пов'язаних з дійсним обчисленням рішень) властивостей диференційних рівнянь.

Завдання стохастичної стійкості виникають у теорії керування при розгляді систем, на які впливають зовнішні неконтрольовані, випадкові впливи. Якщо при цьому відома бажана область роботи системи, то завдання оцінки ймовірності знаходження в цій області є досить практичними.

Розглянемо строго марковский процес х_t, з невипадковою початковою умовою x₀ із непустого відкритої безлічі R, що містить початок координат. Нехай P — деяка безліч, що містить R. Тоді виникає кілька завдань:

(1) чи існує така безліч R, що для деяких заданих r і P для будь-якого хÎR має місце нерівність:

(2) B розвиток завдання (1): чи можна для кожних фіксованих P і r<1 знайти відповідне R?

(3) Знайти оцінку найбільшого багатьох R при фіксованих P і r з завдання (1).

(4) Завдання рівномірної обмеженості: яке значення

,

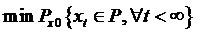якщо P — задана обмежена безліч?

(5) Визначити найменшe безліч, що містить всі межі з імовірністю 1 процесу x_t при t®¥.

(6) Завдання на момент першого виходу: оцінити ймовірність

.

(7) Чи існує кінцевий марковский момент часу t, такий, що x_t®S при t® ¥.

(8) Нехай x = f(x) - p, де p_t - деякий марковский процес. Чи створить пара (x_t,p_t) поворотний процес, тобто такий, у якого ймовірність виходу з довільної області дорівнює 1?

Розглянемо наступні визначення.

Визначення 1. Стан x = 0 називається стійким з вірогідністю 1, тоді і тільки тоді, коли для будь-яких r > 0 і e > 0 існує таке d(r,e) > 0, що

 

, (4.8)

Визначення 2. Система називається стійкою по відношенню до трійки (Q, P, r), тоді і тільки тоді, коли

, (4.9)

Визначення 3. Стан x = 0 у просторі станів називається асимптотично стійкий із імовірністю 1 у тім і тільки тім випадку, коли воно стійко з імовірністю 1 і, крім того, x_t®0 для всіх x₀ з деякої околиці R цієї крапки. Якщо ж R є весь простір, то стан асимптотично стійкий у великому.

Визначення 4. При заданому стані x процес x_t називається рівномірно обмеженим величиною e з імовірністю r у тому випадку, якщо

, (4.10)

Визначення 5. Стан x = 0 в просторі станів називається експоненціально стійким з імовірністю 1 в тому і тільки тому випадку, коли воно стійко з імовірністю 1 і при всіх T < ¥

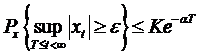, (4.11)

де К< ¥, a> 0.

Визначення 6. Стан x = 0 в просторі станів називається нестійким з імовірністю r в тому і тільки тому випадку, коли

(4.12)

Визначення 7. Процес називається фінально обмеженим з вірогідністю 1 величиною m в тому випадку, коли для кожного x з E існує таке кінцеве (з ймовірністю 1) випадкове час t (x), що

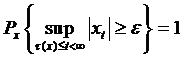, (4.13)

або

, (4.14)

Визначення 8. Позначимо через x_t і x_t¢ процеси, які відповідають початкових умовам x₀ і x₀¢. Процес називається рівно обмеженим з імовірністю 1 в тому випадку, якщо при фіксованій нормеразності ï x-x¢ ï

, (4.15)

рівномірно по х, х¢.

Визначення 9. Процес називається рівномірно стійким з ймовірністю 1 в тому випадку, якщо він задовольняє визначенню 8 і для будь-якого фіксованого e > 0.

, (4.16)

рівномірно по х, х¢.

Основним результатом теорії стохастической стійкості є стохастический аналог теореми Ляпунова про стійкість.

Теорема.

Припустимо, що для деякого m > 0 виконані умови:

1) функція V(x) ненегативна й безперервна на відкритій безлічі Qm = {x:V(x),т};

2) x_t — безперервний праворуч строго марковский процес, певний принаймні до деяких t¢>t_m=inf{t:x_tÏQ_m} з імовірністю 1;

3)нехай Ã — оператор (аналог похідної), певний у такий спосіб:

причому межа задовольняє умові .Позначимо Ã_Qm оператор процесу x_{t tm};

4) функція V(x) належить області визначення оператора Ã_Qm;

5) для будь-якого e > 0 виконано

при t®0.

Нехай також V(0) = 0 і xÎQ_m.

Тоді система стійка стосовно (Q_r,Q_m,1-r/m) при будь-якому r=V(x₀) =V(x)£ m у змісті визначення 2. Крім того, для майже всіх w з маємо

.

Якщо V(x) > 0 при x ¹ 0, xÎQ_m, то початок координат простору станів системи стійко з імовірністю 1.

Дана теорема дозволяє вирішити питання, сформульовані спочатку цього підрозділу.

 

КОНТРОЛЬНІ ПИТАННЯ

 

1) Що означає стійкість системи?

2) B чим розходження понять «рівновага», «стійкість» і «стаціонарність»?

3) Що являє собою рівноважний стан системи?

4) Які виділяються типи стійкості стану системи?

5) Що затверджує теорема Ляпунова про стійкість?

6) Як проводиться класифікація станів рівноваги для систем другого порядку?

7) Що являють собою вузол, сідло, фокус, центр?

8) B чим відмінність поняття стійкості для стохастичних систем?

9) Які випадкові процеси називаються стійкими?

 

РОЗДІЛ 5. НЕСТІЙКІСТЬ І НЕЛІНІЙНІСТЬ ДИНАМІЧНИХ СИСТЕМ