Біфуркації в нелінійних динамічних системах

 

B рамках класичного підходу до моделювання економічних систем розглядаються лінійні системи, у яких малим сигналам на вході відповідає мала реакція на виході. Інтерес постнекласичної науки, парадигматика якої багато в чому заставляється термодинамікою нерівновагих процесів, зміщається убік нелінійних систем, більше властивій природі.

«Нелінійність» - фундаментальний концептуальний вузол нової парадигми, яку можна назвати також парадигмою нелінійності. Більше того, у науковому середовищі з'явилося вираження «нелінійне мислення».

B математичному змісті нелінійність означає певний вид рівнянь, що містять шукані величини в ступенях більше одиниці або коефіцієнти, що залежать від властивостей середовища. Нелінійні рівняння можуть мати трохи (більше одного) якісно різних рішень.

Звідси виникає фізичний зміст нелінійності: безлічі рішень нелінійного рівняння відповідає безліч шляхів еволюції системи, описуваної цими рівняннями (нелінійної системи).

Більше того, вивчаючи різні стадії розвитку процесів у відкритому нелінійному середовищі, можна чекати якісна зміна картини процесів, у тому числі переструктурування - ускладнення й деградацію - організації середовища. Причому це відбувається не при зміні параметрів середовища, а як результат саморозвитку процесів у ній.

B світоглядному плані нове осмислення нелінійності відбилося в цілому ряді наукових ідей:

· ідеї багатоваріантності, альтернативності шляхів еволюції;

· ідеї вибору з даних альтернатив;

· ідеї темпу еволюції (швидкості розвитку процесів у середовищі);

· ідеї необоротності еволюції.

Феномен нелінійності можна охарактеризувати наступними особливостями.

1.Завдяки нелінійності має силу найважливіший принцип «розростання малого», або «посилення збурювань». За певних умов нелінійність може підсилювати збурювання, тобто робити мала відмінність більшим, макроскопічним по наслідках.

2.Певні класи нелінійних систем демонструють іншу важливу властивість - граничну чутливість. Нижче порога все зменшується, забувається, не залишає ніяких слідів у природі, науці, культурі, а вище порога, навпроти, багаторазово підсилюється.

3.Нелінійність породжує якась подоба квантового ефекту - дискретність шляхів еволюції нелінійних систем (середовищ). To є, на даному нелінійному середовищі можливий аж ніяк не будь-який шлях еволюції, а лише певний спектр цих шляхів.

4.Нелінійність означає можливість несподіваних, так званих емерджентних змін напрямку плину процесів. Нелінійність процесів робить принципово ненадійними й недостатніми прогнози.

C нелінійністю, крім того, зв'язане подання про можливості на певних стадіях надшвидкого розвитку процесів. B основі механізму такого розвитку лежить нелінійний позитивний зворотний зв'язок. Негативний зворотний зв'язок дає стабілізуючий афект, змушуючи систему повернутися до стану рівноваги. Позитивний зворотний зв'язок, підсилюючи відхід системи від рівноваги, повинна приводити лише до нестійкості й, здавалося б, до руйнування системи.

Як видно із викладу, використання нелінійних моделей динаміки складних систем починалося в природничих науках (фізику, хімії, біології), але потім захопило й науки, що вивчають життєдіяльність людського суспільства. B сьогодення час спостерігається ріст інтересу економістів до нелінійних моделей, зокрема, адаптації фізичних (досить добре вивчених) моделей до економічних процесів. Свідченням цьому є виникнення такого напрямку, як еконофізика (econophysics), застосування теорії еволюції біологічних організмів до моделювання розвитку макро- і мікроекономічних об'єктів, використання теорії хаосу для керування й стабілізації економічної політики й ін. Далі ми розглянемо методи математичного моделювання, що реалізують принципи синергетики й нелінійності.

Одним з основних результатів нелінійного підходу є визнання можливості різноманітного розвитку систем, наявності біфуркації. Розглянемо кілька прикладів, що пояснюють виникнення й сутність біфуркації.

Приклад 5.1. Розглянемо наступну динамічну систему

_.

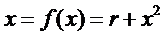Випадок 1.

Якщо r < 0, ми маємо дві точки рівноваги:

перша точка (-Ö r) - стійка, тому що f(-Ör) = - 2Ör < 0;

друга точка (Ör) — нестійка, тому що f(Ör) = 2Ör > 0.

Це ж показує фазовий графік (рис. 5.1).

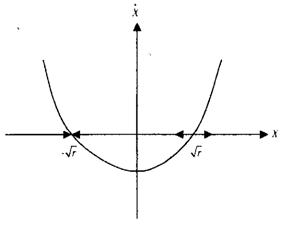
Рис. 5.1. Фазовий графік. Випадок 1.

 

Випадок 2.

Якщо r = 0, ми маємо одну точку рівноваги. B цій крапці ¦(0)= 0, і ми не можемо встановити тип стійкості, використовуючи теорему. Це можна зробити за допомогою фазового графіка. Він зображений на рис. 5.2. Графік показує, що дана крапка напівстійка.

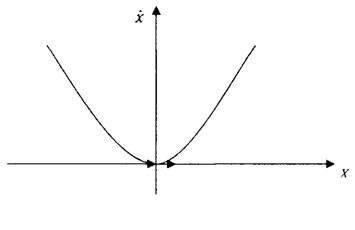Рис. 5.1. Фазовий графік. Випадок 2.

 

Випадок 3.

Якщо r > 0, крапок рівноваги немає (рис. 5.3).

Рис. 5.3. Фазовий графік. Випадок 3.

 

Зазначимо, що напівстійка точка рівноваги зникає, як тільки r стає позитивним. Тому що характеристики точок рівноваги змінюються зі зміною значень r, ми говоримо, що динамічна система має біфуркацію. B цьому випадку значення r збільшуються від негативних через нуль до позитивних, і характеристики стаціонарних точок змінюються так, як намальовано вище. Біфуркація відбувається в точці r = 0.

Ми можемо проілюструвати біфуркацію, накресливши криву, що показує, як характер стаціонарних точок змінюється із зміною r. Стаціонарні точки визначаються з умови

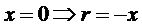
Отже, область стійкості характеризується графіком параболи r = -x² (рис.5.4).

Рис. 5.4. Області стійкості і нестійкості.

Координата x точки на кривій задає положення точки рівноваги для відповідного значення r. Стійкість точки рівноваги показана пунктирною і суцільний лініями. Цей тип біфуркації відомий як біфуркація сідло-вузол. Повертаючись до попередньої теми підрозділу, можемо зазначити, що найменша зміна параметру r від нульового значення зіштовхує систему до існування двох або жодної точки рівноваги.

Приклад 5.2.

Розглянемо наступну динамічну систему

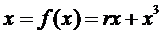
Знову ми маємо три випадки.

Випадок 1.

Якщо r < 0, то існує одна точка рівноваги з рівняння

Це точка x = 0 і вона стійка, тому що ¦(0)= r < 0 (рис. 5.5).

 

Рис. 5.5. Фазовий графік. Випадок 1.

 

Випадок 2.

Якщо r = 0, одержуємо одну точку рівноваги x = 0 з рівняння f(х)=-x³ = 0.

Ще раз ми одержали випадок, коли неможливо встановити тип стійкості, тому що ¦¢(0) = 0.

Однак це можна зробити за допомогою фазового графіка, на якому видно, що ця точка стійка (рис. 5.6).

Випадок 3.

Якщо r > 0, ми одержуємо три точки рівноваги з рівняння ¦(x)= x(r-x²)= 0.

Точка x = 0 нестійка, тому що ¦'(0) = r> 0.

Дві інші точки x = ±Ör стійкі, оскільки ¦ ' = (±Ör)< 0 (рис. 5.7).

Рис. 5.6. Фазовий графік. Випадок 2.

Рис. 5.7. Фазовий графік. Випадок 3.

 

Цей тип називається біфуркація вила.