Лінійні моделі попиту та пропозиції

 

Розглянемо спочатку дискретну модель на прикладі павутино подібної. Нехай ринок якого-небудь окремого товару характеризується наступними функціями попиту та пропозиції: D= D(P), S = S(P).

Для існування рівноваги ціна повинна бути такий, щоб товар на ринку був розпроданий, або D(P) = S(P).

Ціна рівноваги задається цим рівнянням (яке може мати безліч рішень), а відповідний обсяг покупок-продажів, позначуваний через – наступним рівнянням:

.

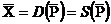Динамічна модель виходить при наявності запізнювання попиту або пропозиції. Найпростіша модель у дискретному аналізі включає незмінне запізнювання або відставання пропозиції на один інтервал:

D_t = D(P_t) і S_t = S(P_t-1).

Це може трапитися, якщо для виробництва розглянутого товару потрібен певний період часу, обраний за інтервал. Дія моделі така: при заданому P_t-1 попереднього періоду обсяг пропозиції на ринку в поточному періоді буде S(P_t-1) і величина P_t повинна встановитися так, щоб був куплений весь обсяг запропонованого товару. Іншими словами, P_t і обсяг покупок-продажів X_t характеризуються рівнянням:

.

Отже, знаючи вихідну ціну P₀, за допомогою цих рівнянь ми можемо одержати значення P₁ і X₁. Потім, використовуючи наявну ціну P₁, з відповідних рівнянь одержимо значення P₂ і X₂, і т.д. Тобто, зміна P_t характеризується різностним рівнянням першого порядку (одноінтервальне відставання):

.

Рішення можна проілюструвати діаграмою, представленої на рис. 6.6, де D і S – відповідно криві попиту та пропозиції, а положення рівноваги (зі значеннями i ) відповідає точці їхнього перетину Q. B динамічнії моделі D має той же зміст, що й у статичнії, але ордината кривій S показує обсяг пропозиції в даний період часу залежно від цін, керуючих ринком у попередній момент часу. Ціна в початковий момент часу дорівнює P₀.

Відповідна крапка Q₀ на кривій S дає обсяг пропозиції в період 1. Весь цей запропонований обсяг товару розкуповується при ціні , що задана крапкою Q₁ на кривій D з тією же ординатою (X₁), що і Q₀. В другий період часу рух відбувається спочатку по вертикалі від точки Q₁ до точки на кривій S, котра дає Х₂, а потім по горизонталі – до точки Q₂ на кривій D. Остання точка характеризує Р₂ . Продовження цього процесу і дає графік павутини, показаний на рис. 6.6.

Рис. 6.6. Графічне рішення павутино подібної моделі попиту і пропозиції

 

Ціни й обсяги (покупок – продажів) у послідовні періоди часу є відповідно координатами точок Q₁, Q₂, Q₃, … Q_n на кривій попиту D. B розглянутому випадку послідовність крапок тяжіє до Q. При цьому крапки по черзі розташовуються на лівій і правій стороні від Q. Отже, і значення ціни P_t прагнуть до , розташовуючись по черзі по обидві сторони від . Точно так відбувається й з обсягами покупок-продажів (X_t). Припустимо, що D іде вниз, a S – нагору. Тоді інтуїтивно ясно, що рух із загасаючими коливаннями виникне, якщо крива D у точці рівноваги Q опускається до осі абсцис ОР крутіше (під більшим кутом), чим крива S. Вибуховий коливальний рух виникає у випадку, коли крива D менш крута стосовно осі OP, чим S (кут нахилу кривої D до осі OP менше кута нахилу S). При рівних кутах нахилу D і S виникають регулярні коливання, тобто незатухаючі й невибухові.

Рішення можна одержати алгебраїчно для випадку лінійних функцій попиту і пропозиції: D = α + aР, S = β + bР. Значення рівноваги і будуть задані рівняннями: , тобто

(6.12)

Дискретна динамічна модель задається рівнянням:

(6.13)

Шукаємо спочатку рішення, що дає рівновагу. Для цього покладемо P_t = і X_t = для всіх значень t:

(6.14)

Одержуємо ті ж значення і , що й в (6.12). Отже, якщо в якому-небудь періоді існували ціни й обсяги, що забезпечували рівновагу, то в динамічній моделі (6.13) вони зберігаються й у наступних періодах. Статична рівновага погоджується із цією моделлю. Віднімемо рівняння (6.14) з (6.13) і покладемо p_t = P_t , x_t = X_t 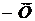. Тоді

(6.15)

Рівняння (6.15) аналогічні (6.13), за винятком того, що вони описують відхилення від рівнів рівноваги (тепер уже відомо, що такі існують). Обидва ці рівняння є різностними рівняннями першого порядку. Покладемо c = b/a і підставимо його в рівняння (6.15), так що різностне рівняння відносно буде: .

При даному значенні р₀ у момент t = 0 рішення легко отримуємо шляхом ітерації:

, .

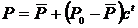Об’єми покупок-продаж в кожний період визначаються із рівняння (6.15).

Зазвичай крива попиту йде вниз (а < 0), a крива пропозиції – нагору (b > 0), тобто c = b/a < 0. B цьому випадку покладемо r = | c | = b/(-a), так що r буде позитивне. Тоді і послідовні значення при t = 0, 1, 2, 3,... будуть відповідно , , 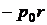, , 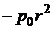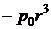…, …, так що приймає по черзі позитивні й негативні значення. Отже, чергуються й знаки P_t, які по черзі будуть розташовуватися вище й нижче . Є наступні три можливості:

1) b > (-а) – кут нахилу S (до OP) більше, ніж кут нахилу D. B цьому випадку r > 1, і ряд послідовних значень є нескінченно зростаючим по абсолютній величині. Отже, P , і має місце вибухове коливання (при чергуванні знаків);

2) b = (-a) – кути нахилу D і S рівні. B цьому випадку r = 1, і ряд значень буде просто складатися із чергування р₀ і (-р₀). Тому 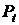буде послідовно більше й менше P на одну й ту саму величину, рівну первісній розбіжності (P₀ – ), тобто буде мати місце регулярне коливання (із чергуванням знаків);

3) b < (-a) – кут нахилу D (до OP) більше, ніж S. B цьому випадку r < 1, і послідовність зменшується по абсолютній величині. Виходить, послідовно ліворуч і праворуч, тобто прагне із загасаючими коливаннями до рівня рівноваги.

B випадку (3), чим більше буде -а стосовно b, тобто чим крутіше D порівняно з S, тим скоріше будуть загасати коливання й тем швидше 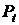буде прагнути до . Початкові збурювання також впливають на амплітуду коливання. Чим далі P₀ від , тим більше буде розмах коливань і тим довший проміжок часу, необхідний для їхнього припинення.

Треба відзначити, що випадок (2) із триваючими й правильними коливаннями настільки рідкий, що його можна вважати майже тривіальним – на базі його не можна побудувати ніякої теорії циклу.

Проведемо аналіз випадку (3). Незважаючи на можливе заперечення, що складається в тім, що загасаючі коливання «нереальні», можна запропонувати дуже простий розвиток моделі (3) із загасаючими коливаннями, що дозволяє представити рух 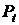із триваючими коливаннями в часі. Для цього замість кривих попиту та пропозиції, незмінних у часі, візьмемо криві, які під впливом зовнішніх сил змінюються в часі або регулярно, або циклічно, або випадково, або як-небудь інакше.

Тоді ще до припинення коливань, показаних на рис. 6.6, яке-небудь зрушення в кривій D або S приведе до збурювання, і коливання з'являться знову. Наприклад, Q₀ могла перебувати в точці рівноваги або поблизу неї до зрушення нагору кривої D до положення, показаному на рис. 6.4. Тоді коливання будуть відбуватися вищеописаним чином, триваючи, скажемо, до крапки Q ₃, де коливальний рух буде порушено зрушенням нагору кривої S. Отже, виникне коливальний рух із ще більшою амплітудою, який поступово припиниться до появи якого-небудь нового збурювання. Для лінійної моделі можливе алгебраїчне тлумачення у випадку паралельного переміщення кривих попиту та пропозиції. Рівняння (6.13) тоді буде мати вигляд:

.

де , характеризують зрушення в момент t = 0, 1, 2, 3,.... Різницевим рівнянням щодо ціни буде:

. (6.16)

Для рішення рівняння (6.16) необхідно лише визначити різницю – , зрушень у часі попиту та пропозиції.

B безперервній моделі ціна є функція часу P(t). Попит та пропозиція (потоки в одиницю часу) суть також функції часу. Попередня павутино подібна модель ураховувала запізнювання пропозиції. Цьому буде грубо відповідати передумова про зміну ціни на стороні попиту, а не пропозиції. Тоді одержимо модель, рівносильну моделі з безперервним запізнюванням пропозиції. Це запізнювання має просту показову форму. D(t) залежить від P і dP/dt, a S(t) – тільки від Р. Модель діє, як і в попередньому випадку, а саме: у кожний момент ціна P установлюється так, щоб попит повністю поглинав пропозицію, то X(t) і P(t) задовольняли рівнянню:

.

Якщо функції лінійні, то

. (6.17)

Приймемо P(t)= і X(t)= для всіх t, тобто для спільного положення рівноваги обох змінних:

. (6.18)

Віднімемо (6.17) з (6.18) і приймемо p = P – і x = X – . Так як dp / dt = dP / dt, то:

. (6.19)

Рівняння (6.17) і (6.18) являють собою диференціальні рівняння першого порядку. Приймемо с = . Тоді диференціальне рівняння відносно P(t) буде мати вигляд: .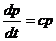

Для рішення помітимо, що 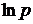. Тоді ln p=c, тобто ln p=const+ct, тобто , або P = + (P₀ – ) .

B звичайному випадку, якщо а < 0, < 0, b > 0, то c < 0, де c = .

Отже, ціна P(t) рухається в часі монотонно до – ціни рівноваги, так як різниця p → 0 подібно показової функції . Менш звичайний випадок, коли також b <0. Але якщо тільки –b<–a, тобто кут нахилу D до осі ОР в площині ОPХ більше, ніж кут нахилу S, то приходимо до того ж результату, що й у першому випадку. Диференційне рівняння цієї моделі має менше рішень, ніж відповідне кінцево-різницеве рівняння, наведене вище.

Розглянуті павутиноподібна й безперервна моделі дуже прості й добре відомі. Вони є частково динамічними, тому що встановлюють співвідношення на ринку тільки одного товару й ураховують ціну лише його одного, а не ціни інших товарів і доходи. Проте, вони містять основні формулювання динаміки й дозволяють розкрити деякі найважливіші властивості, загальні для всіх динамічних моделей попиту та пропозиції. Перелічимо ці особливості.

1. Модель припускає деякі функціональні співвідношення.

B даному випадку це — ринковий попит покупців і пропозиція продавців. Кожне з них представляє функцію ціни. Ці функції є власне кажучи побудовами на основі минулого або очікуваного. Ціна або дана покупцям і продавцям ззовні, або передбачається ними. Попит представляється як планована або передбачувана величина покупок, пропозиція — як планована або передбачувана величина продажів, причому всі ці пропозиції відносяться до початку проміжку часу t. Продавці очікують, що ціна буде такою, як і в попередній період P_t-1 і відповідно припускають продати S = S (P_t-1). Покупці враховують лише фактичну ціну й відповідно до цього планують свої покупки в розмірі D_t = D (P_t).

2. Форма функції також задана. Завдання можемо спростити, розглядаючи окремий випадок при певній формі функції (наприклад, лінійної D = α + aP), або ж взявши наближення до даної формі функції (наприклад, лінійну апроксимацію в обмежений області біля точки рівноваги). Це можна здійснити за допомогою розкладання в ряд Тейлора функції попиту з малоїю різницею P - ;

Прийнята в завданні лінійна (або будь-яка інша) форма повинна бути відповідною і являти собою або гарну апроксимацію, або зручне спрощення. Так, коефіцієнт а, позначений вище, може бути або коефіцієнтом при Р в лінійній функції попиту, або нахилом прямої попиту в точці рівноваги. B останньому випадку він може приблизно відбивати малі варіації Р навколо .

3. Необхідно точно визначити умови, при яких діє модель. Це припускає перехід від очікуваних і планованих величин на основі минулого до реалізованих фактично. Необхідно точно визначити специфічну природу зв'язків між фактичними значеннями змінних і механізм переходу передбачуваних величин у фактичні. B розглянутій моделі з рухом даного товару на одному ринку фактично сформовані відносини характеризуються рівністю покупок і продажів (X_t, по визначенню). Далі, у розглянутому випадку перехід від очікуваних величин до фактичних здійснюється «методом рівноваги», де ціна і є «рівноважною» змінною. На початку періоду t продавці очікують, що ціна буде Р_{t- 1} і пропонують для продажу продукцію S_t. Зміна запасів не передбачається (хоча можливо, що товар є швидкопсувним), так що пропозиція повинна дорівнювати X_t (продаж = покупкам). B процесі встановлення ринкової рівноваги попит стає рівним пропозиції (= продажам = покупкам), тому що ціна досягає такого рівня, при якому пропозиція повністю поглинається. Всі економічні очікування реалізуються. Виключення становить лише ціна P_t-1, яку очікували продавці. Вона не збігається з реалізованою ціною Р_t, що управляє ринком у даному періоді.

За допомогою дуже невеликої модифікації цієї дискретної моделі можна зовсім змінити умови її дії, увівши ступінчасту функцію (метод послідовного порушення рівноваги). B момент t - 1 виробники випускають кількість товарів, що відповідає домінуючій в цей момент ціні P_t-1. B кінці періоду цю масу товарів здобувають торговці, так що її можна продати протягом наступного періоду t (як S_t). B початку періоду t на основі всіх відомих на той момент даних торговці встановлюють ціни продажів Р_t. Покупці тоді вирішують, скільки вони куплять за цими цінами (D_t). B моделі передбачається, що торговці вгадують завжди правильно й встановлюють ціни на такому рівні, при якому вони можуть збути весь запас товарів: S_t = D_t = обсяг покупок-продажів.

B моделі необхідно передбачити й варіювання — як запобіжний захід проти неправильних передбачень цін торговцями. Нехай встановлена ними ціна Р_t така, що D_t перевершує кількість товарів, що продаються S_t. При наявності торговельних запасів попит (дорівнює покупкам-продажам) можна покрити за рахунок їхнього зменшення. Тоді пропозиція, що передбачалася S_t буде менше фактичних продажів і різницю прийдеться покрити за рахунок запасів. B результаті покупці реалізують свої плани (припущений попит = фактичним покупкам), але продавцям прийдеться зробити несподівані вилучення запасів. C іншої сторони, якщо відсутні або малі запаси (наприклад, швидкопсувних товарів), то попит не вдасться задовольнити, і його змушене скорочення вимагатиме обмеження споживання або інших подібних заходів. Тоді передбачуваний попит буде урізаний до величини фактичних покупок, і в покупців виникнуть незаплановані заощадження, продавці ж реалізують свої плани. B більшості моделей зазвичай приймається, що плани покупок реалізуються (очікуваний попит дорівнює фактичним закупівлям), а можливий «розрив» компенсується вкладеннями. Таке припущення може бути розумним або зручним, але, як показує наведений приклад, воно, звичайно, не є необхідним.

4. Умова дії моделі, що задовольняється у фактичних ринкових відносинах, записується у вигляді рівняння з відповідною змінною. B даному випадку ціна є такою рівноважною змінною. Завдання полягає в тім, щоб позбутися від інших змінних (D_t, S_t і звичайно фактичного значення X_t) і зосередити найбільшу увагу на одній (Р_t). Інші змінні (наприклад, X_t) можна знайти, як тільки визначена найважливіша змінна (Р_t). Рівняння павутиноподібної моделі є найпростішою формою різницевого рівняння з одноінтервальним запізнюванням (Р_t і P_t-1 явно входять у рівняння). Шукається рішення цього рівняння. B випадку рівноваги без запізнювання питання зводиться до знаходження одного або декількох значень P, спільних з умовами рівноваги. При наявності запізнювання в кінцево-різницевому рівнянні рішення припускає, що задані й визначені якісь початкові значення або умови, у даному випадку початкова ціна P₀. Рівняння характеризує дію моделі в кожний проміжок часу, але результат протягом часу, узятого в цілому, залежить від існуючої початкової конфігурації, подібно тому, як опущена в автомат монета приводить його в дію. Модель може «стартувати» лише з якогось вихідного положення. Економічно це означає, що зміну ціни в часі можна визначити, лише знаючи початкове порушення рівноваги або відхилення її від положення рівноваги. Той факт, що в даному прикладі потрібно знати лише одне початкове значення, є випадковим. Він являє собою результат існування тільки одноінтервального запізнювання, того, що відповідне кінцево-різницеве рівняння буде першого порядку. При багаторазовому або розподіленому запізнюванні кінцево-різницеве рівняння буде мати більше високий порядок і буде потрібно знати не одне, а кілька початкових значень.

5. Рішення різницевих рівнянь у ряді випадків може бути зведене до методики рішення й аналізу диференціальних рівнянь. Рішення істотно спрощується рекурсивною моделлю. Це означає, що якщо дані всі змінні до (t – 1), то модель забезпечує й одержання одного за іншим значень змінних для інтервалу t. B розглянутому випадку при заданих P_t-1, виходить спочатку X_t = S_t, а потім P_t.

При дослідженні рішень моделей попиту та пропозиції виникають питання, пов'язані з економічною інтерпретацією. Першим завжди виникає наступне питання: чи існує положення рівноваги, сумісне з рівнянням? Відповідь дається підстановкою в рівняння P_t = для всіх t. B даному випадку таке існує, і це є статичний рівень. B інших випадках таке може не існувати. Застосовується й інший штучний прийом: визначивши , простежити не зміну первісної величини P_t, а її відхилення від положення рівноваги, p_t = P_t - . Це має економічний сенс, тому що інтерес представляє саме відхилення від положення рівноваги. Математично найкращий спосіб такого перемикання зводиться до віднімання рівняння, що характеризує точку , з рівняння, що виражає P_t.

Модель із усією очевидністю показує, що статика й динамiка тісно взаємопов’язані. Динамічна модель типу павутинної розглядає рухи навколо положення рівноваги або відхилення від нього. Однак стійке існування положення рівноваги (тобто один раз досягнуте, вона зберігається постійно), спільного з моделлю, зовсім не припускає, що за всяким відхиленням буде відбуватися повернення у вихідне статичне положення. Рух може віддалятися від вихідного статичного положення або бути спрямованим до якогось іншого, відмінного від вихідного. І, навпаки, питання про «стійкість» положення рівноваги в статичному випадку повинне і може розглядатися лише з точки зору динамічної моделі. Положення рівноваги стійке, якщо початкове збурювання породжує повернений динамічний рух до положення рівноваги, а не убік від нього й не до якого-небудь іншого положення.

Безперервна модель має, загалом, ті ж властивості, відрізняючись головним чином в акцентуванні або в деталях. Функції моделі представляють попит та пропозицію залежно від ціни й швидкості зміни останньої. Припущення й плани покупців і продавців представляються такими, що безупинно пристосовуються в часі до руху цін. Ці очікування, щоб бути спільними, повинні являти собою ланки одного ланцюга. Модель, яка виражає співвідношення очікуваних величин попиту та пропозиції, діє знов-таки по методу наближення до положення рівноваги. Ринкові сили безупинно змінюють ціни так, щоб пропозиція була повністю реалізована. Ціна є змінною, що забезпечує рівновагу, що змінюється від одного моменту до іншого для підтримки рівності попиту та пропозиції, будучи спільною для покупок і продажів (потоків у відповідний момент часу). Основне розходження полягає в інтерпретації моделі з точки зору рішень покупців і продавців. B дискретному аналізі одиницею часу був обраний інтервал прийняття рішень або перегляду планів, характерною рисою було розходження між очікуваннями (намірами) і їхнім здійсненням (реалізаціями). Все це загалом зникає в безперервній моделі, тому що передбачається, що прийняття рішень, перегляд їх і пристосування до обстановки, що змінилася, відбувається безупинно. Однак багато властивостей дискретної моделі можна ввести й у безперервну, наприклад запізнювання або зміни запасів.

C математичної точки зору безперервна модель веде до диференціального рівняння відносно який-небудь змінної (у даному випадку P(t)), а не до кінцево-різницевого.