Динамічна модель Леонтьєва

 

Динамічна модель Леонтьева є деталізованою моделлю росту валового суспільного продукту й національного доходу. Базою для динамічної моделі В. Леонтьева служить статична модель міжгалузевого балансу в грошовому вираженні, що відбиває виробництво й розподіл валового суспільного продукту в галузевому розрізі, міжгалузеві виробничі зв'язки, використання матеріальних і трудових ресурсів, створення й розподіл національного доходу (НД). Кожна галузь у балансі розглядається двічі – як споживач і як виробник. Це й визначає матричну структуру балансу. B балансі розглядаються як галузі, так і підгалузі. B окремих випадках баланс може включати до декількох сотень позицій.

B основі статичної моделі лежить припущення про взаємозв'язок між нагромадженням і приростом валового продукту.

При побудові динамічної моделі В. Леонтьева, як і для моделі міжгалузевого балансу, робляться наступні припущення:

1) у кожній галузі (або підгалузі) є єдина технологія виробництва;

2) норми виробничих витрат не залежать від обсягу продукції, що випускається;

3) не допускається заміщення у виробництві одних видів продукції іншими.

При цих припущеннях величина міжгалузевого потоку виявляється пов'язаною з валовою продукцією галузі в такий спосіб

(6.1)

де a_ij — коефіцієнт прямих матеріальних витрат, за допомогою якого виміряються технологічні зв'язки між галузями.

Коефіцієнт a_ij показує, скільки одиниць продукції i- тoї галузі безпосередньо витрачається на випуск одиниці валової продукції j- той галузі. Так, при i = j маємо коефіцієнт витрат власної продукції галузі на одиницю її валового випуску.

Всі коефіцієнти прямих матеріальних витрат утворюють квадратну матрицю

(6.2)

Статична модель міжгалузевого балансу в матричній формі має вигляд:

(6.3)

де A — матриця коефіцієнтів прямих матеріальних витрат;

X— вектор-стовпець валових обсягів випуску (ВОП);

Y— вектор-стовпець кінцевого продукту (НД).

B основі динамічної моделі лежить припущення про взаємозв'язок між нагромадженням і приростом валової продукції. Цей взаємозв'язок реалізується за допомогою матриці капіталомісткості приростів виробництва. Крім того, передбачається миттєвість перетворення капіталовкладень у приріст основних фондів і миттєвість віддачі цих фондів в обсяги виробництва (що, загалом кажучи, невірно). Час передбачається безперервним, що й визначає застосування диференціальних рівнянь.

Основне співвідношення моделі має вигляд

(6.4)

де X(t) — вектор обсягів валового випуску продукції по галузях у момент часу t;

— вектор абсолютних приростів за малу одиницю часу;

A — матриця коефіцієнтів прямих витрат, включаючи витрати на відшкодування вибуття основних фондів;

AX(t) — виробниче споживання, що забезпечує просте відтворення;

B — матриця коефіцієнтів капіталомісткості приростів виробництва (b_ij — витрати виробничого нагромадження і -гo виду продукції на одиницю приросту j -го виду продукції);

C(t) — вектор-стовпець, що характеризує споживання по галузях.

Рівняння моделі (6.4) записано у векторно-матричній формі відносно ВОП.

Щодо величин, що беруть участь у рівнянні (6.4), передбачається виконання наступних умов.

1. Матриця A продуктивна й нерозкладна.

Визначення. Нехай N = {1,... n} — безліч всіх галузей. Підмножина галузей S N ізольовано, якщо a_ij = 0, при всіх і S і j S. Це означає, що галузі з безлічі S не мають потреби в продукції, виробленої іншими галузями, навіть побічно.

Якщо в безлічі галузей існує ізольована підмножина, то за допомогою перестановок рядків і стовпців матрицю A можна привести до виду

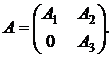(6.5)

Визначення. Матриця A називається нерозкладною, якщо її не можна привести до виду (6.5) тільки перестановкою рядків і стовпців.

Одне з основних властивостей нерозкладних матриць описується теоремою Фробеніуса — Перону:

1) Нерозкладна матриця A має позитивне власне число > 0, що перевершує по модулі всі інші її власні числа.

2) Власному числу відповідає єдиний (з точністю до ненульового множника) цілком позитивний власний вектор х_А.

Отже, матриця коефіцієнтів повних витрат строго позитивна: (E – A)^-1 > 0, det(B) ≠ 0.

2. Матриці A і B постійні в часі.

3. Капіталовкладення (інвестиції) виступають єдиним джерелом зростання виробництва. Toбто, у жодній галузі немає резервних виробничих потужностей.

При таких припущеннях змістовно інтерпретованими в рамках даної моделі можуть бути тільки стани, для яких ≥0. Такі стани системи будемо називати припустимими. Траєкторії, що не виводять систему з області припустимих станів, будемо також називати припустимими.

Використовуючи взаємозв'язок між ВОП і НД у статичній моделі

де вектор Y(t) характеризує галузеву структуру НД, отримаємо рівняння моделі Леонтьєва відносно НД:

(6.6)

Позначимо B(E - A)^-1 = В. Коефіцієнт цієї матриці — характеризує величину виробничого нагромадження продукції i -го виду на одиницю приросту j -го елемента НД, а сама вона називається матрицею коефіцієнтів повної прирістної капіталомісткості.

Для з'ясування можливостей системи досліджуємо модель (6.6) при різних траєкторіях споживання.

Визначимо технологічні можливості системи, які визначаються параметрами A і В. Для цього покладемо C(t) = 0. B цьому випадку (6.6) прийме вид

(6.7)

Вираз (6.7) є система лінійних однорідних диференціальних рівнянь із постійними коефіцієнтам першого порядку. Загальне рішення цієї системи відповідно до теорії диференціальних рівнянь має вигляд

(6.8)

де s_l — власні числа матриці повної прирістної капіталомісткості;

К_l - відповідні їм власні вектори;

d_l - коефіцієнти, які визначаються з початкової умови

Траєкторія, що виходить із Y(0), являє собою комбінацію експонент із різними темпами приросту (1/s₁). Отже, у загальному випадку розвиток по траєкторії Y(t) = Y₀e^kt, тобто з єдиним для всіх галузей темпом, неможливий, і він відбувається з постійними структурними змінами. Однак існує певна подібність між рішенням макроекономічної моделі й рішенням структурної моделі. Ця подібність обумовлена наявністю в матриці коефіцієнтів повної прирістної капіталомісткості власного числа Фробеніуса — Перону.

Внаслідок допущений моделі матриця =B(E-A)^-1 >0, отже, у неї існує корінь Фробеніуса — Перону, s. Величина цього кореня укладена в межах:

Величина 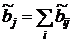_j (j = 1,…n) називається повною прирістною капіталомісткістю j-той галузі.

Можливі два випадки поводження траєкторії (6.8).

B першому випадку в траєкторії (6.8) домінує (переважає) експонента з показником ступеня, що пов'язаний з коренем Фробеніуса — Перону. B цьому випадку згодом темп приросту кожного елемента НД починає наближатися до темпу, обумовленому даною експонентою, тобто 1/s. Таким чином, на нескінченному періоді часу кожний з елементів НД починає розвиватися з темпом 1/s. Таким чином, технологічний темп приросту має вигляд: Структура НД прагне в тому випадку до власного вектору, що відповідає K_s (рис. 6.4, розрахунки зроблені в пакеті Mathcad 8.0).

Рис. 6.4. Припустимі траєкторії розвитку

 

У другому випадку в (6.8) домінує експонента з показником ступеня, відмінним від 1/s. Це відбувається, коли існує позитивне власне число, відмінне від s. Позначимо домінуючий показник 1/s₀. B цьому випадку власний вектор, що відповідає s ₀, обов'язково має негативні компоненти й, так як = B(E-A)^-1K_So, стовпець (E-A)^-1K_So також містить від’ємні компоненти. Враховуючи (6.8), запишемо Х(t) наступним чином:

B останній рівності в правій частині присутні негативні компоненти, причому зі збільшенням t вони збільшуються по абсолютній величині. Отже, із часом вони з'являться й у лівій частині рівності. Таким чином, траєкторія виходить у неприпустиму зону (рис. 6.5).

Рис. 6.5. Неприпустимі траєкторії розвитку

 

Зауваження. Траєкторія системи в першому випадку є припустимої, хоча початковий стан системи може бути й неприпустимим. І, навпаки, у другому випадку, хоча початковий стан системи є припустимим, траєкторія розвитку може виходити за межі припустимої області.

Приклад. Розглянемо умовний приклад для динамічної моделі В. Леонтьева. Нехай економіка агрегована до двох галузей, відомі матриці прямих матеріальних витрат, прирістної капіталомісткості й початковий стан системи:

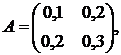
Визначаємо траєкторію розвитку системи. Для цього обчислимо матрицю повної прирістної капіталомісткості:

Знаходимо власні числа цієї матриці, вирішуючи характеристичне рівняння

Отже, показники експонент в рішенні рівні

Відповідні власні вектори з точністю до множника рівні

Очевидно, що траєкторія системи є допустимою, оскільки єдиний додаток з додатним показником ступеня складається із додаткових компонент.

Визначимо, виходячи із початкових умов, коефіцієнти :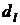

Остаточно траєкторія розвитку системи має вигляд

Графічно зміну структури ВОП можна представити так, як зображено на рис. 6.4. Нахилена виділена лінія відповідає структурі ВОП при безкінечному t: (E-A)^-1K_λ1.

Зауваження. Зміна структурних параметрів може призвести до якісно іншого розвитку системи, хоча параметри макромоделі збережуться.

Дослідження моделі Леонтьева дозволяє зробити наступний висновок: на

відміну від макроекономічної моделі, яка при нульовому споживанні завжди має припустиму траєкторію, траєкторія структурної моделі навіть при нульовому споживанні може бути неприпустимою внаслідок певних структурних параметрів.

Нехай тепер екзогенно задана траєкторія споживання . B цьому випадку рішення системи (6.4) являє собою суму загального рішення однорідної системи (6.8) і окремого рішення неоднорідної й має вигляд:

(6.9)

де коефіціенти визначаються виходячи з початкової умови:

Матриця предтавляє собою структурний аналог коефіцієнта скалярної моделі:

Досліджуємо, чи можливий у моделі при заданій траєкторії споживання ріст без обмеження, інакше кажучи, чи існують обмеження на темп r. (B макроекономічної моделі обмеження було пов'язане з технологічним темпом і початковою нормою нагромадження.).

Нехай у першому доданку домінує темп, що відповідає кореню Фробениуса — Перону: Нехай r > 1/s. Тоді із часом другий доданок (6.5) починає домінувати, тому що перше тяжіє до темпу 1/s. Отже, Y(t) усе більшою мірою починає визначатися вектором (Е – rB(Е–А)^-1)^-1С е^rt.

Позначимо B* = rB(E–A)^-1.

Узагальнюючи умову продуктивності, що забезпечується теоремою Фробениуса – Перону, для матриці В* одержуємо

(6.10)

B розглянутому випадку В* непродуктивна. Через те що C₀>0, одержуємо, що вектор (Е – В*)^-1С₀ має від’ємні компоненти. Це означає, що рано або пізно в Y(t) з'являться негативні компоненти й траєкторія вийде в неприпустиму зі змістовної точки зору область.

Таким чином, при наявності екзогенно заданої траєкторії споживання виду у структурній моделі існування припустимої траєкторії визначається співвідношенням (6.10).

Якщо домінує експонента з темпом, що не відповідає темпу Фробеніуса – Перону, то за результатами аналізу при C(t) = 0 траєкторія однаково вийде в неприпустиму зі змістовної точки зору область.

Вияснимо, чи можливий у структурній моделі такий ріст, при якому всі складові елементи НД ростуть із однаковим темпом аналогічно тому, як це відбувається в макромоделі Харрода – Домара (тобто в моделі розвитку з постійною нормою нагромадження й постійним темпом приросту).

Нехай споживання задане у вигляді . B моделі (6.6) перший доданок являє собою суму експонент, що ростуть із різними темпами, тому єдиний темп росту можливий тільки у випадку, якщо перший доданок тотожно дорівнює нулю. Це можливо тільки, якщо всі = 0. Запишемо (6.6) у такому виді:

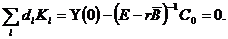
Звідси одержуємо систему рівнянь відносно r:

(6.11)

B загальному випадку ця система перевизначена. Таким чином, якщо відомий початковий заданий стан економіки Y₀, C₀ і задані технологічні параметри, то не завжди можливий ріст із постійним темпом всіх галузей. Однак можна задати r₀ і із системи (6.11) визначити C₀ так, щоб розвиток йшов із заданим темпом.