Перейдемо тепер до більш складних, нелінійних, моделей, що описують виникнення циклічних коливань в економічному розвитку. Починаючи із простої моделі, запропонованої Гудвіном, будемо послідовно її ускладнювати, враховуючи все більшу кількість факторів.
Будемо вважати, що в будь-який момент часу t економіка має у своєму розпорядженні основний капітал К, що включає заводи, устаткування тощо, його обсяг змінюється зі швидкістю, яка дорівнює відношенню чистих капіталовкладень до загального зношування за даний період часу. Джерелом економічного доходу є обсяг виробництва Y і споживання С. Ці величини зв'язані між собою співвідношеннями
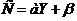 ; (7.1)
; (7.1)
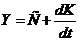 . (7.2)
. (7.2)
де а й 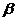 — дійсні контрасти, такі, що а < 0,
— дійсні контрасти, такі, що а < 0, 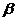 < С. З рівняння (7.1) видно, що між обсягом виробництва й споживанням існує лінійна залежність. Рівняння (7.2) означає, що вся випущена продукція, що, або споживається, або йде на розширення виробництва. Припустимо далі, що основним капіталом К управляють так, щоб підтримувати на рівні, пропорційному обсягу виробництва. Якщо R — бажаний рівень основного капіталу в момент часу t, то
< С. З рівняння (7.1) видно, що між обсягом виробництва й споживанням існує лінійна залежність. Рівняння (7.2) означає, що вся випущена продукція, що, або споживається, або йде на розширення виробництва. Припустимо далі, що основним капіталом К управляють так, щоб підтримувати на рівні, пропорційному обсягу виробництва. Якщо R — бажаний рівень основного капіталу в момент часу t, то
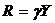 , (7.3)
, (7.3)
де 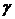 – деякий параметр.
– деякий параметр.
Представимо перший варіант моделі. З рівнянь (7.1) та (7.2) випливає, що
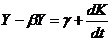 (7.4)
(7.4)
звідки
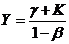 (7.5)
(7.5)
Зі співвідношення (7.3) видно, що періодичне поводження величини Y (або K) може виникнути як наслідок коливань у капіталовкладенні К. B свою чергу, ці коливання виникають із прагнення зрівняти величини К та R (бажаний рівень основного капіталу). Нехай проводиться екстремальна політика капіталовкладень:
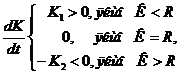 (7.6)
(7.6)
де К1 і К2 не залежать від часу t.
Розглянемо сутність формули (7.6). Якщо основний капітал менше бажаного рівня, то умова (7.6) відповідає максимальному рівню капіталовкладень (перша умова в (7.6)). Якщо ж бажаний рівень перевищений, то капіталовкладення нульові, а основний капітал амортизується зі швидкістю K2 (третя умова (7.6)). Розумно допустити, що при максимальному рівні капіталовкладень швидкість, з якої можуть будуватися нові підприємства, більше швидкості амортизації й старіння, тобто
К1 > К2 . (7.7)
З рівнянь (7.3) – (7.6) слідує, що
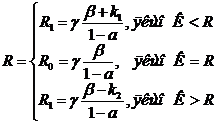 (7.8)
(7.8)
Нехай R2 < K < R1, так що при t = 0 виконується R = R1. Тоді рівень капіталовкладень дорівнює 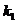 > 0, величина k зростає, а Y залишається постійною (рис. 7.1) до тих пір, поки не досягнеться рівність K = R1. Тоді R приймає значення R0. , тому що K = R. Тепер К = R1 > R = R0., і показник R миттєво стає рівним R2. Таким чином, К миттєво змінюється від величини
> 0, величина k зростає, а Y залишається постійною (рис. 7.1) до тих пір, поки не досягнеться рівність K = R1. Тоді R приймає значення R0. , тому що K = R. Тепер К = R1 > R = R0., і показник R миттєво стає рівним R2. Таким чином, К миттєво змінюється від величини 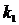 до -k2, a R — від R1 до R2. B той же самий момент, відповідно до формули (7.5), різко падає обсяг виробництва. Тепер К зменшується до величини R2. Аналогічне міркування показує, що R при цьому стає рівним R1, так що K = R2 < R = R1, і величина K знову стає рівною
до -k2, a R — від R1 до R2. B той же самий момент, відповідно до формули (7.5), різко падає обсяг виробництва. Тепер К зменшується до величини R2. Аналогічне міркування показує, що R при цьому стає рівним R1, так що K = R2 < R = R1, і величина K знову стає рівною 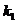 . Основний капітал K знову зростає до R1, і цикл замикається. Таким чином, обидві величини – K й Y – зазнають коливання, як показано на рис. 7.1.
. Основний капітал K знову зростає до R1, і цикл замикається. Таким чином, обидві величини – K й Y – зазнають коливання, як показано на рис. 7.1.
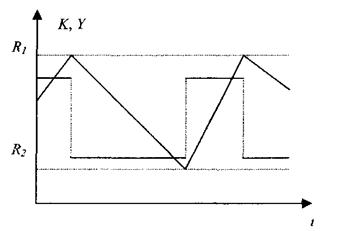
Рис. 7.1. Коливання величин K і Y у часі для політики
капіталовкладень виду «стій – іди»
Розглянемо поведінку моделі на фазовій площині (K, K), що представлена на рис. 7.2. Рух відбувається по прямолінійних відрізках BCі DA, де K = k1 і К = – k2 відповідно. Стрибки від A до B і від C до D відповідають розривам функції Y, що показані на рис. 7.1.
Дана модель добре зображує економічний цикл. Під час періодів капіталовкладення обсяг виробництва високий і економіка перебуває в періоді підйому. Коли ж капіталовкладення відсутні, обсяг виробництва падає, і економіка перебуває в стані депресії. Однак у розглянутій моделі є багато недоліків. Так, стрибки в капіталовкладенні й миттєва реакція на них з боку обсягу виробництва Y (див. формулу (7.5)) не відповідають дійсності. Крім того, з умови k1 = k2 видно, що періоди спаду значно перевищують періоди підйому, чого в реальності не спостерігається. Більше того, у моделі відсутнє загальне зростання економіки, тому що обсяг виробництва, основний капітал та інші показники періодично приймають колишні значення.
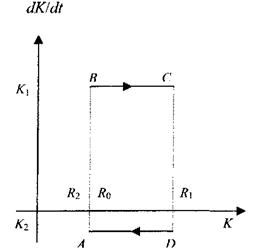
Рис. 7.2. Подання стану економіки на фазовій площині
(стрибки величин зазначені пунктиром)
Приведемо другий варіант моделі. Модифікуємо модель, з огляду на такі фактори:
1) вплив капіталовкладень на збільшення обсягу виробництва;
2) відсутність стрибкоподібних змін у капіталовкладенні.
Для урахування першого фактора змінимо рівняння (7.5) так, щоб в функції Y не було стрибків навіть у тому випадку, коли величина K їх має. Це можна зробити замінивши рівняння (7.5) на
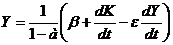 , (7.9)
, (7.9)
де 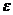 – деяка позитивна константа.
– деяка позитивна константа.
Зрозуміло, що новий додаток в (7.9) спричиняє затримку в реакції функції Y на зміну K. З рівняння (7.9) знаходимо:
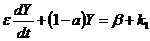 , якщо K > R, (7.10)
, якщо K > R, (7.10)
 , якщо K < R. (7.11)
, якщо K < R. (7.11)
Приймемо, що в момент часу t = t 1 депресія закінчується і відбувається миттєвий перехід від (7.11) к рівнянню (7.10), тоді залежність величини Y від часу t для фази підьому буде мати вид:
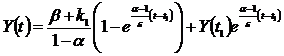 (7.12)
(7.12)
З рішення (7.12) видно, що величина Y не зростає миттєво до значення 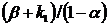 , a прагне до нього при t
, a прагне до нього при t 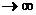 . Помітимо, що час, який потрібний для того, щоб функція Y(t) із заданою точністю стала дорівнювати цій величині, цілком залежить від параметра
. Помітимо, що час, який потрібний для того, щоб функція Y(t) із заданою точністю стала дорівнювати цій величині, цілком залежить від параметра 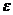 . Аналогічним чином, рівняння (7.11) згладжує стрибкоподібне падіння Y(t) (див. рис. 7.1) наприкінці періоду підйому.
. Аналогічним чином, рівняння (7.11) згладжує стрибкоподібне падіння Y(t) (див. рис. 7.1) наприкінці періоду підйому.
Ліквідуємо тепер розриви в капіталовкладенні, тобто «пом'якшимо» раптовий перехід від K = k1 до К = -k2 (і навпаки), що виникає, коли K стає рівним R.
Розглянемо ту частину капіталовкладень, що виникає зі зміною обсягу виробництва. Зміна в капіталовкладенні відбувається тому, що ми хочемо підтримувати основний капітал на рівні бажаного капіталу. Зміна величини Y викликає зміну R, що, у свою чергу, тягне зміну K. Зрозуміло, що якби нам вдалося підтримувати K = 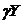 , то виконувалося б і співвідношення K = R. Але такого бути не може, оскільки рівність не може виконуватися при всіх значеннях t, тому що величина K має верхню межу k1 і нижню межу (– k2). Тому ми припустимо, що K =
, то виконувалося б і співвідношення K = R. Але такого бути не може, оскільки рівність не може виконуватися при всіх значеннях t, тому що величина K має верхню межу k1 і нижню межу (– k2). Тому ми припустимо, що K = 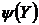 . Вид функції
. Вид функції 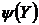 зображений на рис. 7.3.
зображений на рис. 7.3.
Як видно з рисунку, вимушені капіталовкладення 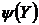 близькі до ідеального рівня
близькі до ідеального рівня 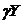 для малих величин Y, а при великих
для малих величин Y, а при великих 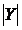 вони обмежені величинами k1 к (– k2). Помітимо, що функція
вони обмежені величинами k1 к (– k2). Помітимо, що функція 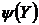 –
– 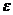 Y немонотонна (тобто має «горби») і схожа на кубічну параболу. Коли капіталовкладення досягають свого максимального значення, основний капітал перестає задовольняти вимозі K =
Y немонотонна (тобто має «горби») і схожа на кубічну параболу. Коли капіталовкладення досягають свого максимального значення, основний капітал перестає задовольняти вимозі K = 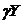 .
.
Це означає, що K треба вибрати у вигляді:
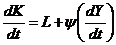 , (7.13)
, (7.13)
де 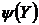 – індуковані капіталовкладення, викликані зміною обсягу виробництва, L – вплив інших капіталовкладень.
– індуковані капіталовкладення, викликані зміною обсягу виробництва, L – вплив інших капіталовкладень.
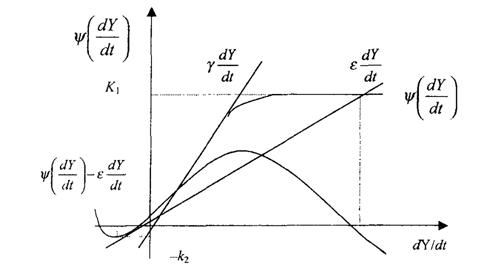
Рис. 7.3. Вимушені капиталовкладення 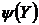
Тоді рівняння (7.9) треба замінити на:
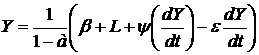 (1.14)
(1.14)
Щоб одержати графік функції Y залежно від Y, потрібно зрушити функцію 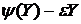 , що зображена на рис 7.3, на величину
, що зображена на рис 7.3, на величину 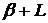 і поділити на (1 – а). Якщо величина
і поділити на (1 – а). Якщо величина 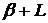 достатньо велика, то отримаємо графік, подібний до наведеного на рис. 7.4.
достатньо велика, то отримаємо графік, подібний до наведеного на рис. 7.4.
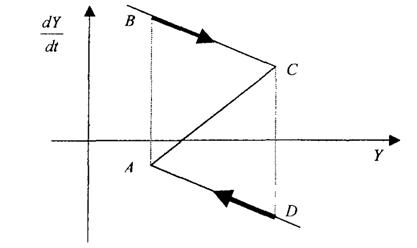
Рис. 7.4. Поведінка другої моделі на фазовій площині, рух відбувається тільки по немонотонній характеристиці
Ця крива, разом із передумовою про стрибки, повністю описує поведінку другої моделі. Крапки, що відповідають всім можливим станам моделі, лежать на цій кривій, і знак показує, зростає або убуває величина Y. Таким чином, рух крапки, що визначає стан системи, повинне відбуватися в напрямках, зазначених стрілками. Отже, крапка (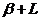 ; 0) є нестійкою нерухомою крапкою системи. Із крапок C і A за аналогією з рис. 7.2 повинні відбуватися стрибки. Припустивши, що стрибки відбуваються із A в B і з C в D, одержимо релаксаційні коливання для Y.
; 0) є нестійкою нерухомою крапкою системи. Із крапок C і A за аналогією з рис. 7.2 повинні відбуватися стрибки. Припустивши, що стрибки відбуваються із A в B і з C в D, одержимо релаксаційні коливання для Y.
Тепер розглянемо третій варіант моделі. Урахуємо тепер запізнювання реальних капіталовкладень відносно ухвалення рішення про їхню необхідність. Це означає, що індуковані вкладення в момент часу t насправді залежать не від Y(t), а від Y(t – v), де v — запізнювання.
Тоді замість рівняння (7.14) треба писати:
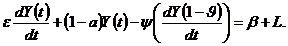 (7.15)
(7.15)
Якщо ввести 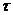 = t – v, з (7.15) одержимо:
= t – v, з (7.15) одержимо:
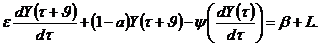 (7.16)
(7.16)
Розкладемо ліву частину рівняння (7.16) по ступенях u та збережемо лише члени першого порядку по v. Тоді знаходимо:
 (7.17)
(7.17)
Або
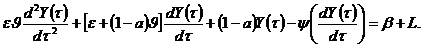 (7.18)
(7.18)
Якщо вважати, що 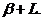 = const і ввести:
= const і ввести:
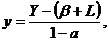 (7.19)
(7.19)
то (7.18) можна переписати у вигляді:
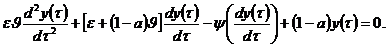 (7.20)
(7.20)
Введемо нову залежну і незалежну змінні співвідношеннями:
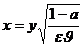 (7.21)
(7.21)
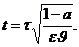 (7.22)
(7.22)
Тоді замість (7.20) маємо:
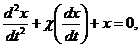 (7.23)
(7.23)
де  (7.24)
(7.24)
Якщо  , то функція
, то функція 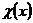 схожа на кубічну параболу, а (7.23) – рівняння типу рівняння Релея
схожа на кубічну параболу, а (7.23) – рівняння типу рівняння Релея
 (7.25)
(7.25)
і в нього є стійкий граничний цикл, тобто мають місце автоколивання.
 2018-01-08
2018-01-08 784
784








