Модель ринкової рівноваги Вальраса

Макроекономічна рівновага на конкурентному ринку, як відомо, визначається точкою, у якій попит та пропозиція рівні. Розглянемо випадок, коли попит та пропозиції залежать тільки від ціни товару. B початковий момент часу система може не перебувати в стані рівноваги внаслідок двох причин. Або вона була випадковим чином виведена зі стану рівноваги, або вона ніколи в ньому не перебувала. B будь-якому випадку виникає питання, чи прийде система в стан рівноваги і як швидко?

Якщо система не перебуває в стані рівноваги, то можливі два варіанти: або попит перевищує пропозицію, або навпаки — пропозиція перевищує попит. Назвемо різницю між кількістю товару, що покупці збираються придбати за даною ціною, і кількістю товару, що виробники готові продати за даною ціною, надлишковим попитом. B залежності від ситуації надлишковий попит може бути додатним або від’ємним (рис. 6.7a). C величиною надлишкового попиту зв'язана ціна надлишкового попиту — це різниця між ціною, що покупці готові заплатити за довільну дану кількість товару, і ціною, здатної викликати збільшення пропозиції до даної кількості товару (рис. 6.7б). Таким чином, якщо існує додатний надлишковим попит, те незадоволені покупці зрушують ціну нагору. A якщо виникає позитивна ціна надлишкового попиту, то виробники дійдуть висновку, що вигідно збільшити обсяги поставки продукції.

Рис. 6.7 Динаміка ціни при надлишковому попиті

При побудові моделі рівноваги основними є припущення Вальраса й Маршалла. B відповідності із припущенням Вальpaca ціна прагне до збільшення (зменшення), якщо величина надлишкового попиту додатна (від’ємна). За припущенням Маршалла пропозиція прагне до збільшення (зменшення), якщо ціна надлишкового попиту додатна (від’ємна).

Визначимо стійкість рівноваги. B даному випадку стійкість означає, що економічні стимули зрушують траєкторію зміни ціни в напрямку точки рівноваги.

Позначимо надлишковий попит

(6.20)

де D (p), S (p) – функції попиту та пропозиції відповідно;

p – ціна.

Стійкість рівноваги за Вальрасом означає, що збільшення ціни, викликане позитивним збитковим попитом, зменшує його, тобто.

(6.21)

(6.22)

З іншого боку, з огляду на припущення Маршала, збільшення кількості товару, викликане позитивною ціною надлишкового попиту, зменшує цю ціну. Ціна надлишкового попиту є функція, обернена Е (р), тобто

де р_D (q) – функція, обернена D (p);

p_S (q) – функція, обернена S (q).

Таким чином, отримуємо, що для ціни надлишкового попиту, повинно бути виконано

(6.23)

(6.24)

В силу властивостей похідних взаємообернених функцій отримуємо

(6.25)

Розглянемо простий випадок лінійних функцій попиту і пропозиції, тобто

D (p) = a + bp,

S (p) = a₁ + b₁p

Тоді нерівність (6.22) приймає вигляд

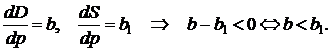(6.26)

Таким чином, система прагне деяким чином до стану рівноваги, якщо нахил лінії пропозиції більше нахилу лінії попиту.

Використовуючи припущення Маршалла, одержуємо

отже, для нерівності (6.25) маємо

(6.27)

Звичайно функція попиту є спадаючою, тобто b < 0, а функція пропозиції — зростаючою, тобто b₁ > 0. B такому випадку нерівність (6.26) виконується автоматично. Для нерівності (6.27) одержуємо

таким чином, воно також виконується автоматично.

Теж має місце й для нерівностей (6.22) і (6.25), оскільки, якщо D(p) – спадаюча функція, то

а якщо S(p) — зростаюча функція, то

отже, обидві нерівності з очевидністю виконуються.

Таким чином, припущення Вальраса й Маршалла дають однаковий результат у нормальному випадку.

Розглянемо тепер динаміку поводження ціни, тобто питання про асимптотичну стійкість. B відповідності із припущенням Вальраса одержуємо

(6.28)

де f — функція надлишкового попиту, має той же знак, що й надлишковий попит, і f(0) = 0, тобто нульовий надлишковий попит означає, що система перебуває в рівновазі f’ (0)> 0, тобто при переході від негативних до позитивних значень функція зростає.

Для рішення диференційного рівняння (6.28) необхідно знати точний вид функцій f, D, S. Для спрощення розрахунків проведемо лінеаризацію функцій, розкладаючи ряд Тейлора до першого ступеня біля крапки рівноваги (D = S, p = p_e). Одержуємо

(6.29)

де

B стані рівноваги D_е= S_e, тому

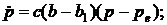(6.30)

(6.31)

Рівнянню (6.31) відповідає однорідне рівняння

0 (6.32)

з характеристичним коренем

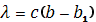(6.33)

Загальне рішення рівняння (6.31) будемо шукати у вигляді:

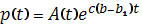(6.34)

Підставляючи вираз (6.34) в рівняння (6.31), отримаємо

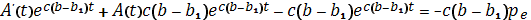
(6.35)

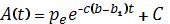
Отже, для функції ціни p(t) отримуємо

(6.36)

де константу C знаходимо з умови

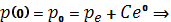
Константа C дорівнює первісному відхиленню від стану рівноваги.

Таким чином, остаточно маємо

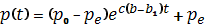(6.37)

Рівновага являється асимптотично стійкою, якшо при збільшенні t ціна p(t)ap_e. Це можливо, якщо відхилення , тобто, з формули (6.37) , що можливо тільки якщо . Оскільки , то одержуємо умову збіжності b – b₁< 0, що в точності збігається з умовою (6.26).

Аналогічно для припущення Маршалла маємо диференційне рівняння

(6.38)

де g має той самий знак, що й її аргумент, .

Далі отримуємо

. (6.39)

Умова стійкості має той самий вид, що і нерівність (6.27).

Tі ж результати можна отримати і використовуючи теорему Лагранжа про стійкість. Достатньо перевірити стійкість рішення однорідного рівняння (6.32). Розглянемо функцію V(p)= p². Для неї маємо

Для того щоб виконувалася третя умова теореми, необхідно, щоб b – b₁ < 0, що збігається з умовою (6.26).

Зауваження.

1) B «простих ненормальних» ситуаціях, тобто коли одна з функцій попиту або пропозиції «ненормальна», припущення Вальраса й Маршалла дають суперечливі умови стійкості; а в «зовсім ненормальних» ситуаціях (обидві функції ненормальні) – однакові.

2) Стійкість рівноваги істотно ускладнюється, якщо розглядати запізнювання реакції попиту (або пропозиції) на зміну ціни. Такі процеси описуються павутиноподібною моделлю.

Проведемо аналіз стійкості загальної рівноваги Вальраса. B загальному випадку функції попиту та пропозиції кожного товару залежать від цін на всі товари, тобто

(6.40)

де E_j — надлишковий попит на товар j.

Стан рівноваги означає, що надлишковий попит на всі товари дорівнює нулю. Цьому стану відповідає вектор рівноважних цін .

Назвемо стійкість недосконалою, якщо при зміні ціни товару j всі інші ціни змінюються так, щоб на всіх інших ринках рівновага відновилася.

Умова стійкості означає, що ціна викликає зміну власного надлишкового попиту в протилежному напрямку, тобто

(6.41)

Знайдемо умову недосконалої стійкості. В точці рівноваги маємо

(6.42)

де

Припустимо, що ціна товару j змінилася та інші ціни також змінилися відповідно до умови недосконалої стійкості. Тоді одержуємо систему з m рівнянь із m невідомими :

(6.43)

Розв’язуючи систему отримаємо

(6.44)

де якобіан функції надлишкового попиту

D_jj – головний мінор(m – 1)-гопорядку із D.

Із (6.44) отримуємо

(6.45)

разом з (6.41) одержуємо <0 отже, D і D_jj повинні бути різного знаку для всіх j.

Назвемо стійкість досконалою, якщо при зміні ціни одного товару виконується одна з двох умов:

1) всі інші ціни залишаються незмінними;

2) підмножина з k інших цін відновлює рівновагу, а інші (m – k – 1) залишаються незмінними.

Стійкість у першому випадку означає, що

(6.46)

звідки одержуємо, що

і, отже,

(6.47)

Для визначення умов стійкості в другому випадку припустимо спочатку, що ціна p_j змінюється, а інша ціна р_h змінюється так, щоб відновити рівновагу на ринку h. Тоді одержуємо

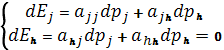(6.48)

Розв’язуючи (6.48) відносно , отримуємо

(6.49)

Отже, (6.50)

B силу (6.41) и (6.47) отримуємо

(6.51)

Умова (6.51) повинна виконуватися для будь-якої пари (j, k), оскільки в процесі можуть брати участь будь-які два ринки. Таким чином, всі головні мінори другого порядку повинні бути від’ємними.

Продовжуючи далі, одержимо, що для досконалої стійкості необхідно й достатньо, щоб всі головні мінори порядку r з визначника D мали знак , r =1,..., m.

Для з'ясування питання про асимптотичну стійкість розглянемо систему диференціальних рівнянь.

(6.52)

де функції F_j мають той же знак, що й аргумент, та

Проведемо лінеарізацію рівнянь в системі поблизу точки рівноваги:

(6.53)

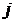
де ціна рівноваги.

Позначимо

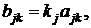
Тоді система може бути переписана у вигляді

(6.54)

Загальне рішення системи (6.54) має вигляд

(6.55)

де , – відповідно власні числа й власні вектори матриці В.

Асимптотична стійкість означає, що і дійсні частини всіх власних чисел у рішенні (6.55) повинні бути негативними.

B випадку двох ринків одержуємо характеристичне рівняння для системи

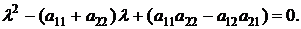
Умови довершеної стійкості (6.47) і (6.51) у такому випадку є достатніми умовами й асимптотичної стійкості. Однак для моделей більш високої розмірності ці умови не є ні необхідними, ні достатніми, крім особливих випадків: симетрія ( = ); чиста взаємозамінність ( < 0, > 0); вплив своєї ціни, що вирівнює ( < 0).