2018-01-08
233
Целью выборочного наблюдения является определение параметров генеральной совокупности (генеральной средней 
и генеральной доли 
) на основе параметров выборочной совокупности (выборочной средней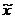 
и выборочной доли w). Разница между генеральными и выборочными параметрами 
называется ошибкой выборки. Её значение при собственно случайном и механическом отборе рассчитывается по формулам:
| Оцениваемый параметр | Повторный отбор | Бесповторный отбор |
| Средняя | 
| 
|
| Доля | 
|  
|
Предельная ошибка выборки 
определяет собой 
- кратную среднюю ошибку 
, где - коэффициент доверия, определяемый по таблице значений интегральной функции Лапласа при заданной доверительной вероятности:
| Доверительная вероятность | 0,683 | 0,950 | 0,954 | 0,990 | 0,997 |
| Коэффициент доверия | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
Необходимая численность выборки, обеспечивающая требуемую точность расчета оценок генеральных параметров при собственно случайном и механическом отборе, определяется формулами:
| Оцениваемый параметр | Повторный отбор | Бесповторный отбор |
| Средняя | 
| 
|
| Доля | 
| 
|
В приведенных формулах 
- дисперсия признака в генеральной совокупности (или дисперсия выборочной совокупности 
, или дисперсия определенная другим возможным способом); 
- дисперсия доли в генеральной совокупности (или дисперсия доли в выборочной совокупности 
, или максимально возможная дисперсия альтернативного признака 
); 
- численность выборки, 
- численность генеральной совокупности.
