ТП 4: Если у – величина бесконечно большая, то  - бесконечно малая.
- бесконечно малая.
ТП 5: Если у – величина бесконечно малая, то  - бесконечно большая, у ≠ 0.
- бесконечно большая, у ≠ 0.
Например:
1) Вычислить: Lim 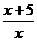
х → 1+ 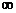
Решение:
Т.к. числитель и знаменатель дроби 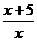 являются бесконечно большими величинами при х→
являются бесконечно большими величинами при х→  , то пределов числителя и знаменателя не существует,
, то пределов числителя и знаменателя не существует,
поэтому разделим каждое слагаемое числителя на знаменатель:
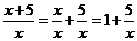 , тогда
, тогда
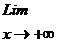
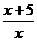 =
= 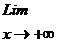 (1 +
(1 + 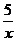 ) =
) = 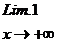 +
+ 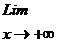
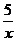 = 1 + 5 x Lim
= 1 + 5 x Lim  = 1 + 5 x 0 =1,
= 1 + 5 x 0 =1,
x→ + 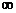
т.к дробь  при х → +∞ является бесконечно малой величиной и следовательно ее предел равен нулю.
при х → +∞ является бесконечно малой величиной и следовательно ее предел равен нулю.
Ответ: Lim 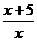 = 1.
= 1.
х → 1+ 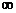
2) Найти: Lim 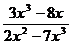
х → 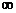
Решение:
Числитель и знаменатель выражения, стоящего под знаком предела при х→  являются бесконечно большими величинами, поэтому для того, чтобы можно было применить теоремы о пределах, предварительно разделим числитель и знаменатель дроби на старшую степень х:
являются бесконечно большими величинами, поэтому для того, чтобы можно было применить теоремы о пределах, предварительно разделим числитель и знаменатель дроби на старшую степень х:
Lim 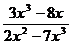 = Lim
= Lim  = Lim
= Lim 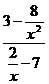 =
=  .
.
х → 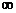 х →
х → 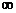 х →
х → 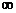
Т.к. под знаком предела стоит дробь, то нужно выяснить, отличен ли от нуля предел знаменателя:
Lim  = Lim
= Lim 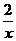 - Lim 7 = 2 x Lim
- Lim 7 = 2 x Lim  - 7 = 2 x 0 – 7 = -7,
- 7 = 2 x 0 – 7 = -7,
x→∞ x→∞ x→∞ x→∞
т.к.  при безграничном возрастании х является величиной бесконечно малой и следовательно Lim
при безграничном возрастании х является величиной бесконечно малой и следовательно Lim  = 0. Предел знаменателя отличен от нуля, следовательно:
= 0. Предел знаменателя отличен от нуля, следовательно:
x→∞
 =
=  =
=  =
= 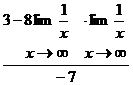 =
=  = -
= - 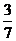
Ответ: Lim 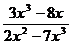 = -
= - 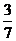
х → 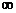
Задание 1.
1.01 Lim 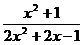 ;
;
x→+∞
1.02 Lim  ;
;
x→+∞
1.03 Lim  ;
;
x→ -2
1.04 Lim 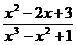 ;
;
x→ 4
1.05 Lim 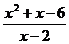 ;
;
x→ 2 
1.06 Lim 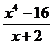 ;
;
x→ -2
1.07 Lim (х2 – 4х + 5);
x→ 5
1.08 Lim 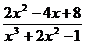 ;
;
x→∞
1.09 Lim 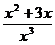 ;
;
x→ 2
1.10 Lim  .
.
x→ 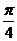
Производная.
I. Определение функции и основные понятия.
Определение 1: Пусть Х и У – некоторые числовые множества. Функцией f называется множество упорядоченных пар чисел (х; у) таких, что х є Х, у є У. Каждый х входит в одну и только одну пару этого множества, а каждый у входит по крайней мере в одну пару. При этом говорят, что числу х поставлено в соответствие число у и пишут у = f (x).
Число у называется значением функции f в точке х.
Переменную у называют зависимой переменной, а переменную х – независимой переменной (или аргументом);
Множество Х называют областью определения (или существования) функции, а множество У – множеством значений функции.
Способы задания функции:
- при помощи формулы (аналитически);
- таблицей;
- графиком;
- договоренностью.
Разность двух значений аргумента называется приращением аргумента:
Δ х = х2 – х1
Разность значений функции, соответствующих значениям х2 и х1 аргумента, называют приращением функции:
Δ f = f( х2 ) – f( х1 )
Определение 3: Производной функции у = f (x) по независимой переменной х в точке х0 называется предел при Δ х → 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует):
f '( х0 ) = Lim  = Lim
= Lim 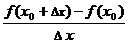
Δ х→0 Δ х→0
Процесс вычисления производной называется дифференцированием.
Определение 2: Функция называется непрерывной в точке х0, если предел функциии ее значение в этой точке равны: Lim f(x) = f(x0).
х →х0
Геометрический смысл производной:
Производная функции f(x) в точке х0 равна угловому коэффициенту касательной к графику функции f(x) в точке (х0; f(х0)).
Физический смысл производной:
Мгновенная скорость движения есть производная от пройденного пути S по времени t.
ук = f '( х0 )(х – х0) + f( х0 )
Таблица правил и основных формул дифференцирования.
Если u и v – некоторые функции от х, имеющие производные при рассматриваемых значениях х, а с – постоянная, то:
I. (u ± v)' = u' ± v'
II. (u · v)' = u' · v + v' · u
III. (c · u)' = c · u'
IV. 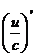 =
= 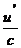
V. 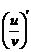 =
=  , v ≠ 0
, v ≠ 0
VI. (c)' = 0
VII. (x)' = 1
Д – постоянная величина
VIII. (xn)' = n · xn -1
IX. (sin x) ' = cos x
X. (cos x) ' = - sin x
XI. (tg x) ' = 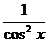
XII. (ctg x) ' = - 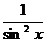
XIII. (Loga x) ' = 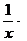 Loga e =
Loga e = 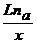
XIV. (Loge x) ' = (Ln x) ' = 
XV. (ax) ' = ax · Ln a
XVI. (ex) ' = ex
XVII. (arcsin x) ' = 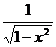
XVIII. (arccos x) ' = - 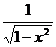
XIX. (arctg x) ' = 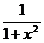
XX. (arcctg x) ' = - 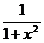
Например:
1. (3100)' = 0 (VI)
2. (12х)' = 12 (III, VII)
3. (x121)' = 121 · x120 (VIII)
4. (2x15)' = 2 · 15 · x15 -1 = 30 х14(III, VIII)
5. (22x) ' = 22x · Ln 22 (XV)
6. (14 sin x) ' = 14 cos x (III, IX)
7. (25 cos x) ' = - 25 sin x (III, X)
8. (7 tg x) ' = 7 · 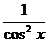 =
= 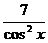 (III, XI)
(III, XI)
9. (5 ctg x) ' = 5 · ( - 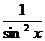 ) = -
) = - 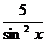 (III, XII)
(III, XII)
10. (х10 – arcsin x)' = (x10)' - (arcsin x)' = 10 x3 - 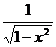 (I, VIII, XVIII)
(I, VIII, XVIII)
11. (x · sin x)' = (x)' · sin x + x · (sin x)' = 1 · sin x + x · cos x = sin x + x · cos x
12. 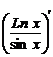 =
=  =
= 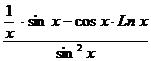 =
=
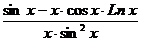 (V, XIV, IX)
(V, XIV, IX)
13. (4x5 – 7 cos x + tg x – ctg x)' = (4x5)' - (7 cos x)' + (tg x)' – (ctg x)' = 4(x5)' –
7(cos x)' + 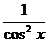 - ( -
- ( - 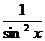 ) = 4 · 5 · x5-1 – 7 · (- sin x) +
) = 4 · 5 · x5-1 – 7 · (- sin x) + 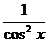 +
+ 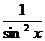 = 20x4 + 7 sin x +
= 20x4 + 7 sin x + 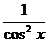 +
+ 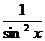 (I, III, VIII, X, XI, XII)
(I, III, VIII, X, XI, XII)
 2018-01-08
2018-01-08 1275
1275
